Evaluate Reverse Polish Notation
Evaluate the value of an arithmetic expression in Reverse Polish Notation.(后波兰式)
Valid operators are +, -, *, /. Each operand may be an integer or another expression.
Some examples:
["2", "1", "+", "3", "*"] -> ((2 + 1) * 3) -> 9 ["4", "13", "5", "/", "+"] -> (4 + (13 / 5)) -> 6
public class Solution {
public int evalRPN(String[] tokens) {
Stack<String> data = new Stack<String>();
//Stack<String> oper = new Stack<String>();
if(tokens.length == 0){
return 0;
}
for(int i = 0 ; i < tokens.length;i++ ){
if(tokens[i].equals("+") || tokens[i].equals("-") || tokens[i].equals("*") || tokens[i].equals("/")){//如果是表达式
String res = operate(data.pop(),tokens[i],data.pop());
data.push(res);
}else{//如果是操作数九直接入栈
data.push(tokens[i]);
}
}
return Integer.parseInt(data.pop());
}
public String operate(String a , String c,String b){
switch(c){
case "+":
return String.valueOf(Integer.parseInt(b) + Integer.parseInt(a));
case "-":
return String.valueOf(Integer.parseInt(b) - Integer.parseInt(a));
case "*":
return String.valueOf(Integer.parseInt(b) * Integer.parseInt(a));
case "/":
return String.valueOf(Integer.parseInt(b) / Integer.parseInt(a));
}
return "";
}
}
中缀表达式转换为后缀表达式(http://www.nowamagic.net/librarys/veda/detail/2307)
我们把平时所用的标准四则运算表达式,即“9+(3-1)*3+10/2"叫做中缀表达式。因为所有的运算符号都在两数字的中间,现在我们的问题就是中缀到后缀的转化。
中缀表达式“9+(3-1)*3+10/2”转化为后缀表达式“9 3 1-3*+ 10 2/+”
下面我们来具体看看这个过程。
1. 初始化一空栈,用来对符号进出栈使用。
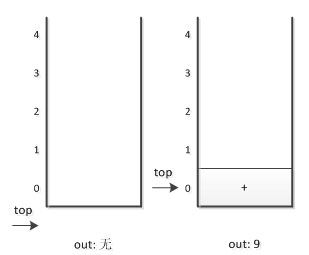
2. 第一个字符是数字9,输出9,后面是符号“+”,进栈。
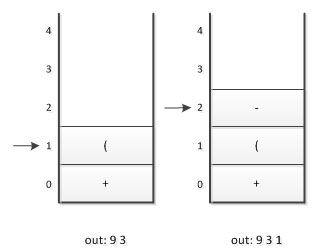
3. 第三个字符是“(”,依然是符号,因其只是左括号,还未配对,故进栈。
4. 第四个字符是数字3,输出,总表达式为9 3,接着是“-”进栈。
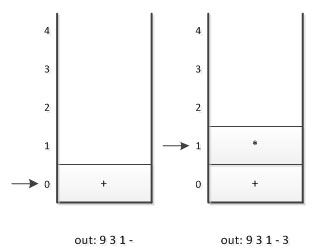
5. 接下来是数字1,输出,总表达式为9 3 1,后面是符号“)”,此时,我们需要去匹配此前的“(”,所以栈顶依次出栈,并输出,直到“(”出栈为止。此时左括号上方只有“-”,因此输出“-”,总的输出表达式为9 3 1 -
6. 接着是数字3,输出,总的表达式为9 3 1 - 3 。紧接着是符号“*”,因为此时的栈顶符号为“+”号,优先级低于“*”,因此不输出,进栈。
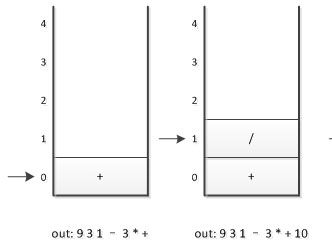
7. 之后是符号“+”,此时当前栈顶元素比这个“+”的优先级高,因此栈中元素出栈并输出(没有比“+”号更低的优先级,所以全部出栈),总输出表达式为 9 3 1 - 3 * +.然后将当前这个符号“+”进栈。也就是说,前6张图的栈底的“+”是指中缀表达式中开头的9后面那个“+”,而下图中的栈底(也是栈顶)的“+”是指“9+(3-1)*3+”中的最后一个“+”。
8. 紧接着数字10,输出,总表达式变为9 3 1-3 * + 10。
9. 最后一个数字2,输出,总的表达式为 9 3 1-3*+ 10 2
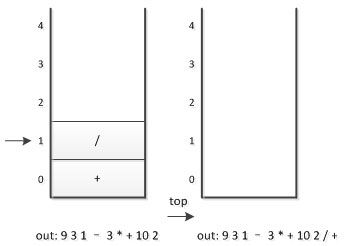
10. 因已经到最后,所以将栈中符号全部出栈并输出。最终输出的后缀表达式结果为 9 3 1-3*+ 10 2/+
- 将中缀表达式转化为后缀表达式(栈用来进出运算的符号)。
- 将后缀表达式进行运算得出结果(栈用来进出运算的数字)。
整个过程,都充分利用了找的后进先出特性来处理,理解好它其实也就理解好了栈这个数据结构。