数据结构与算法2-栈与队列实现 (stack and queue implementation)
数据结构与算法2-栈与队列实现 (stack and queue implementation)
写在前面
本节动手实践栈与队列的编写,包括数组实现的栈ArrayStack,链表实现的栈LinkedListStack,固定大小\动态扩容的数组实现的循环队列,以及优先级队列。下一节讨论基于栈与队列的算法应用。
1.栈的实现
栈的结构特性为: 最后进入栈的最先出栈,即所谓的LIFO(,last in first out)特性。
栈的形象比喻就是一叠盘子,放在最上面的最先拿走使用,只要还有足够空间,即这一叠盘子不是太高,就可以继续往上面堆盘子。
栈的实现本身不复杂,可以使用数组或者链表来实现。
我们约定抽象数据类型ADT栈的操作列表如下:
template<typename T>
class Stack
{
public:
virtual ~Stack(){};
virtual void push(T data)=0;
virtual T pop()=0;
virtual bool isEmpty()=0;
virtual void clear() = 0;
virtual T getTop()=0;
virtual int getSize()=0;
};
1.1 数组实现的栈
数组实现的栈,注意可以固定大小,也可以动态扩容。这里我们选择根据需要动态扩充容量,当入栈需要动态扩容时,由于需要复制栈中原先元素,因此时间复杂度变为O(n),通常情况下入栈操作复杂度为O(1)。
我们定义栈如下:
class ArrayStack : public Stack<T>
{
public:
ArrayStack(int cap=initCapacity);
~ArrayStack();
//公共接口函数省略
private:
void resize(int cap);
private:
T *base,*top;
int capacity;
};
其中base指针指向数组首地址,top指向栈顶的下一位置;当top-base >= 栈容量capacity时则需要动态扩充容量。
注意 :容量是值为数组分配的实际空间,而size或者下文队列的length则是指实际放置元素的个数。
这里着重强调下元素入栈操作,定义为:
template<typename T,int initCapacity>
void ArrayStack<T,initCapacity>::push(T data)
{
if(top - base >= capacity) //stack size over capacity
{
resize(2*capacity); //resize as needed
}
*top++ = data;
}
动态扩容函数定义为:
template<typename T,int initCapacity>
void ArrayStack<T,initCapacity>::resize(int cap)
{
if(cap <= capacity)
return;
int size = top - base;
T* mem = 0;
try
{
mem = new T[cap];//reallocate memory
}
catch (const std::bad_alloc& ba)
{
std::cerr << "stack out of memory " << ba.what() <<std::endl;
delete[] base;
throw;
}
if(mem != 0)
{
std::copy(base,base+size,mem); //copy elements
delete[] base; //release old memory
base = mem; //reset base
top = base+size; //reset top
capacity = cap; //update capacity
}
}
测试结果为:
push 1-7 get top: 7 pop top: 7 get top: 6 pop top: 6 stack size: 5 clear stack stack isEmpty: yes push 1-7 pop till empty: 7 6 5 4 3 2 1
1.2 基于链表实现的栈
这里我们不再从头到尾编写链表类来实现了,而是借助于C++提供的链表来实现C++提供的链表实现为双链表。选择用链表表头作为栈顶,则入栈和出栈的操作复杂度都为O(1)。
使用链表的好处就在于,根据需要分配空间,提供了空间的很好管理。
完整定义如下:
#ifndef _LINKED_LIST_STACK_H_
#define _LINKED_LIST_STACK_H_
#include <list>
template<typename T>
class LinkedListStack : public Stack<T>
{
public:
~LinkedListStack()
{
//let std::list do for us
}
void push(T data)
{
list.push_front(data);
}
T pop()
{
T data = list.front();
list.pop_front();
return data;
}
bool isEmpty()
{
return list.empty();
}
void clear()
{
list.clear();
}
T getTop()
{
return list.front();
}
int getSize()
{
return list.size();
}
private:
std::list<T> list;
};
#endif
测试结果同上。
2.普通队列实现
普通队列结构,即为从队尾加入元素,从队头移除元素的线性结构,这称之为先进先出(FIFO first in first out)的结构。
队列可以形象的解释为生活中的排队,例如食堂窗口买饭菜排队,医院缴费窗口排队。
队列可以用数组和链表来实现。利用数组实现时,可以实现固定大小的队列,也可以动态扩容;链表实现则提供了比较好的空间管理。
队列的ADT数据接口定义如下:
template<typename T>
class Queue
{
public:
virtual ~Queue(){}
virtual void enqueue(T data) = 0;
virtual T dequeue()= 0;
virtual void clear()=0;
virtual int getLength()= 0;
virtual bool isEmpty()=0;
};
2.1数组实现的队列-循环队列
为什么使用循环队列?
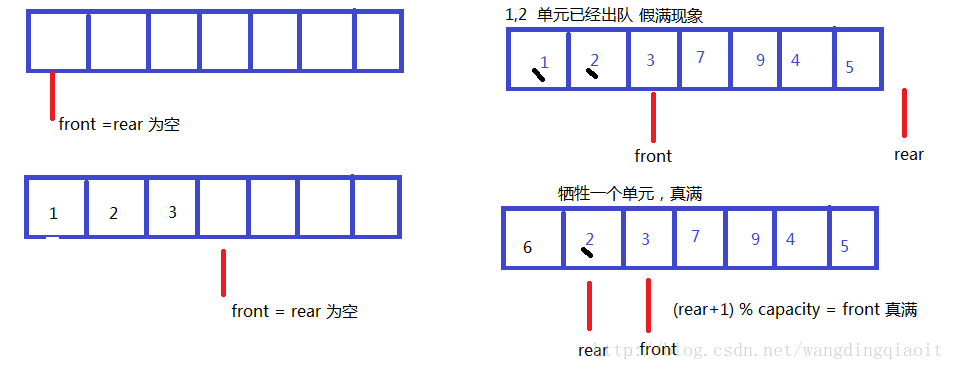
数组实现的队列里用front和rear两个整数索引来保存队列状态,当出现下图所示的情况时即为队列“假满”现象。
出现假满现象时,即是分配再多空间,也会导致空间的为充分利用,此时采取两种方法:
第一,采取固定大小的数组,实现为循环队列;
第二,不采用固定大小,实现为循环队列,仅仅当数组出现真满现象时,才进行容量扩充。
第一种方式则需要提供一个检验队列是否为真满的函数isFull,第二种情况同上述栈实现时一样需要定义resize函数。
固定大小的循环队列ArrayQueue入队操作为:
void enqueue(T data)
{
if((rear+1)% maxCapacity == front)
{
std::cerr<<"logic error : enqueue at full queue. "<<std::endl;
throw std::logic_error ("enqueue at full queue");
}
queue[rear] = data;
rear = (rear+1) % maxCapacity;//rear point to the next of the last
}
动态扩容的循环队列ResizingArrayQueue入队操作为:
void enqueue(T data)
{
if((rear+1)% capacity == front) //queue full
{
resize(2*capacity); // resize as needed
}
queue[rear] = data;
rear = (rear+1) % capacity;//rear point to the next of the last
}
template<typename T,int initCapacity>
void ResizingArrayQueue<T,initCapacity>::resize(int cap)
{
T* mem = 0;
try
{
mem = new T[cap]; //allocate memory
}
catch (const std::bad_alloc& ba)
{
std::cerr << "queue out of memory " << ba.what() <<std::endl;
delete[] queue;
throw;
}
if(mem != 0)
{
if(front < rear)
{
std::copy(queue+front,queue+rear,mem);//copy from front to rear
}else if(front > rear)
{
//note source and destination pointer
std::copy(queue+front,queue+capacity,mem);//copy from front to end
std::copy(queue,queue+rear,mem+capacity-front);//copy from 0 to rear
}
int length = (rear-front+capacity) % capacity;
delete[] queue; //release old memory
queue = mem; //reset queue pointer
front = 0; //reset front index
rear = length; //reset rear index
capacity = cap; //update capacity
}
}
测试结果为:
enqueue 1-10 queue length: 10 dequeue: 1 dequeue: 2 clear queue enqueue 1-10 dequeue till empty: 1 2 3 4 5 6 7 8 9 10
2.2 链表实现的队列
利用C++ list实现的队列更简单,定义如下:
#ifndef _LINKED_LIST_QUEUE_H_
#define _LINKED_LIST_QUEUE_H_
#include <list>
#include "Queue.h"
template<typename T>
class LinkedListQueue : public Queue<T>
{
public:
void enqueue(T data)
{
list.push_back(data);
}
T dequeue()
{
T data = list.front();
list.pop_front();
return data;
}
void clear()
{
list.clear();
}
int getLength()
{
return list.size();
}
bool isEmpty()
{
return list.empty();
}
private:
std::list<T> list;
};
#endif
测试结果同上。
3.优先级队列实现
优先级队列的结构特点为: 队列出队不再以入队先后作为唯一标准,而是根据实际需要定义的谓词函数,该函数表明以怎样方式判定优先级,总是选择优先级最高的元素出队。
优先级队列的形象解释为: 公路收费亭,优先让警车、救护车、消防车通过;超市购物时可能优先为物件很少的顾客先结账;操作系统中选择预估耗时最短的进程先运行等等。
因为每次总是选择优先级最高的元素出队,对于链表实现方式,有两种:
第一种,每次插入元素时根据优先级寻找合适位置插入,优先级从队首到队尾依次降低,出队列时总是从队首选择优先级最高元素出队。这种方式下插入时复杂度为O(n),出队时复杂度为O(1)。
第二种,每次插入时总是加在链表的尾部,但是出队时总是选择优先级最高的元素出队,因此插入时间复杂度为O(1),出队时复杂度为O(n)。
两者在整体上复杂度相同。
对于数组实现方式,相应的也有两种:
第一种,数组元素从队首到队尾优先级降序排列,每次插入时总保持这个顺序,则插入时比较次数最坏为n次,此时移动元素次数为0;当比较次数最好为1次时,移动元素次数却为n;时间复杂度为O(n)。出队时总是选择队首元素出队即可,时间复杂度为O(1)。这种方式可以使用front指针指向队首,rear指针指向队尾,还是可以实现为循环队列情况的。
第二种,数组元素用一个index指向队尾下一个可用位置,数组元素保持无序,仅当需要出队时选择一个优先级最高者出队,然后将最后一个元素移动到出队元素的位置,更新index让其仍然指向下一个可用位置。这种方式入队为O(1),出队为O(n)。当然这种方式的优点是,无序移动过多的元素,最多移动一个元素,即将队尾元素移动到出队元素位置。
这里仅实现为数组的第二种方式,这种方式不再需要front指针,也不必实现为循环队列了,只用一个index索引即可。
这里利用C++的函数对象(function object ),实现优先级比较的谓词函数,默认采用std::less<T>作为谓词函数。关于C++ compare谓词的使用请查阅参考资料部分的[4][5]。
完整定义如下:
#ifndef _PRIORITY_QUEUE_H_
#define _PRIORITY_QUEUE_H_
#include <functional> // std::less
#include <exception>
#include "Queue.h"
#define INIT_LENGTH 16
template<typename T,typename Compare=std::less<T> >
class PriorityQueue : public Queue<T>
{
public:
PriorityQueue():index(0),capacity(INIT_LENGTH)
{
queue = new T[capacity];
}
void clear()
{
index = 0;
}
int getLength()
{
return index;
}
bool isEmpty()
{
return index == 0;
}
T dequeue();
void enqueue(T data);
private:
void resize(int cap);
private:
T* queue;
int capacity;
int index;
};
template<typename T,typename Compare>
void PriorityQueue<T,Compare>::enqueue(T data)
{
if(index >= capacity)
{
resize(2*capacity); //resize as needed
}
queue[index] = data;
index++;
}
template<typename T,typename Compare>
T PriorityQueue<T,Compare>::dequeue()
{
if(index == 0)
{
std::cerr<<"logic error : dequeue at empty queue. "<<std::endl;
throw std::logic_error("dequeue at empty queue");
}
//pick up one with highest priority
int highIndex = 0;
for(int i = 1;i < index ;i++) // O(n)
{
if( Compare()( queue[i],queue[highIndex] ) )
highIndex = i;
}
T result = queue[highIndex];
index--;
queue[highIndex] = queue[index]; //put the last element to the removed position
return result;
}
template<typename T,typename Compare>
void PriorityQueue<T,Compare>::resize(int cap)
{
T *mem = 0;
try
{
mem = new T[cap];
}
catch (const std::bad_alloc& ba)
{
std::cerr << "queue out of memory " << ba.what() <<std::endl;
delete[] queue;
throw;
}
if(mem != 0)
{
std::copy(queue,queue+index,mem); //copy elements
delete[] queue; //release old memory
queue = mem; //reset queue pointer
capacity = cap; //update capacity
}
std::cout<<"resized "<<std::endl;
}
#endif
测试代码如下:
#include <iostream>
#include <string>
#include <functional> // std::less std::greater
#include "PriorityQueue.h"
class Person
{
public:
// default constructor
Person() : age(0) {}
Person(int age, std::string name) {
this->age = age; this->name = name;
}
bool operator <(const Person& rhs) const
{
return this->age < rhs.age;
}
int age;
std::string name;
};
void testIntegers()
{
PriorityQueue<int,std::greater<int> > queue;
int i = 0;
while(i++ < 10)
queue.enqueue(i);
std::cout<<"dequeue till empty: "<<std::endl;
while(!queue.isEmpty())
std::cout<<queue.dequeue()<<"\t";
std::cout<<std::endl;
}
void testPerson()
{
PriorityQueue<Person> queue;
queue.enqueue(Person(24,"Calvin"));
queue.enqueue(Person(30,"Benny"));
queue.enqueue(Person(28,"Alison"));
std::cout<<"dequeue till empty: "<<std::endl;
while(!queue.isEmpty())
{
Person p = queue.dequeue();
std::cout<<p.age<<", "<<p.name<<std::endl;
}
std::cout<<std::endl;
}
int main(int argc, char *argv[])
{
testIntegers();
testPerson();
return 0;
}
测试结果:
enqueue 1-10: dequeue till empty: 10 9 8 7 6 5 4 3 2 1 dequeue till empty: 24, Calvin 28, Alison 30, Benny
测试结果的解释:
上述测试代码中,测试int类型元素时使用std::greater<int>,则队列按照数值大则优先级高的判定准则,元素出队是按照数值从大到小排列;在测试Person类时默认使用std::less<Person>,则会使用Person类重载的<操作符函数作为谓词函数,Person类中指定为年龄小者优先级高,因此元素出队时按照年龄从小到大排列。
参考资料:
[1] 《数据结构与算法 c++版 第三版》 Adam Drozdek编著 清华大学出版社
[2] 《数据结构》 严蔚敏 吴伟明 清华大学出版社
[3] Queues and Priority Queues[4] C++ concepts: Compare
[5] STL Sort Comparison Function