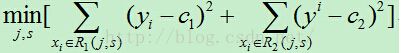CART回归树和GBDT

CART 分为回归树和决策树。这里重点讲讲回归树的特征选择。

回归树选择特征的方法是：平方误差最小化。

具体步骤为：

1）依次遍历每个特征j，以及该特征的每个取值s，计算每个切分点（j,s）的损失函数，选择损失函数最小的切分点。

其中c1,c2分别为R1,R2区间内的输出平均值。

2）使用上步得到的切分点将当前的输入空间划分为两个部分

3）然后将被划分后的两个部分再次计算切分点，依次类推，直到不能继续划分。

4）最后将输入空间划分为M个区域R₁,R₂,…,R_M,生成的决策树为：

其中c_m为所在区域的输出值的平均值

总结：此方法的复杂度较高，尤其在每次寻找切分点时，需要遍历当前所有特征的所有可能取值，假如总共有F个特征，每个特征有N个取值，生成的决策树有S个内部节点，则该算法的时间复杂度为：O(F*N*S)。

下面说GBDT

 GBDT(Gradient Boosting Decision Tree) 又叫 MART（Multiple Additive Regression Tree)，是一种迭代的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终答案。GBDT主要由三个概念组成：Regression Decistion Tree（即DT)，Gradient Boosting（即GB)，Shrinkage (算法的一个重要演进分枝）。

一、 DT：回归树 Regression Decision Tree

GDBT是由回归树组成的。

二、 GB：梯度迭代 Gradient Boosting

Boosting，迭代，即通过迭代多棵树来共同决策。这怎么实现呢？难道是每棵树独立训练一遍，比如A这个人，第一棵树认为是10岁，第二棵树认为是0岁，第三棵树认为是20岁，我们就取平均值10岁做最终结论？--当然不是！且不说这是投票方法并不是GBDT，只要训练集不变，独立训练三次的三棵树必定完全相同，这样做完全没有意义。之前说过，GBDT是把所有树的结论累加起来做最终结论的，所以可以想到每棵树的结论并不是年龄本身，而是年龄的一个累加量。GBDT的核心就在于，每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学。这就是Gradient Boosting在GBDT中的意义，简单吧。

三、Shrinkage 

Shrinkage（缩减）的思想认为，每次走一小步逐渐逼近结果的效果，要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它不完全信任每一个棵残差树，它认为每棵树只学到了真理的一小部分，累加的时候只累加一小部分，通过多学几棵树弥补不足。用方程来看更清晰，即

没用Shrinkage时：（yi表示第i棵树上y的预测值， y(1~i)表示前i棵树y的综合预测值）

y(i+1) = 残差(y1~yi)， 其中： 残差(y1~yi) =  y真实值 - y(1 ~ i)

y(1 ~ i) = SUM(y1, ..., yi) 意思是：前i颗数的预测值的总和为最后预测值。

Shrinkage不改变第一个方程，只把第二个方程改为： 

y(1 ~ i) = y(1 ~ i-1) + step * yi

 

即Shrinkage仍然以残差作为学习目标，但对于残差学习出来的结果，只累加一小部分（step*残差）逐步逼近目标，step一般都比较小，如0.01~0.001（注意该step非gradient的step），导致各个树的残差是渐变的而不是陡变的。直觉上这也很好理解，不像直接用残差一步修复误差，而是只修复一点点，其实就是把大步切成了很多小步。本质上，Shrinkage为每棵树设置了一个weight，累加时要乘以这个weight，但和Gradient并没有关系。这个weight就是step。就像Adaboost一样，Shrinkage能减少过拟合发生也是经验证明的，目前还没有看到从理论的证明。

 GBDT工作过程实例。

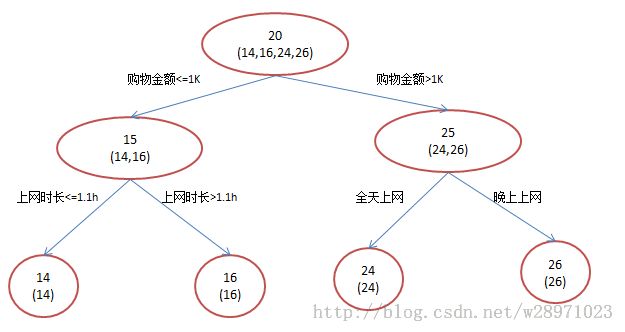
还是年龄预测，简单起见训练集只有4个人，A,B,C,D，他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生；C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练，会得到如下图1所示结果：

 

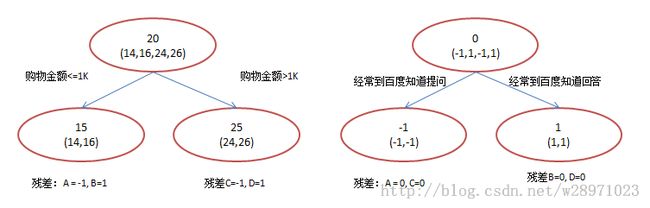
现在我们使用GBDT来做这件事，由于数据太少，我们限定叶子节点做多有两个，即每棵树都只有一个分枝，并且限定只学两棵树。我们会得到如下图2所示结果：

 

在第一棵树分枝和图1一样，由于A,B年龄较为相近，C,D年龄较为相近，他们被分为两拨，每拨用平均年龄作为预测值。此时计算残差（残差的意思就是： A的预测值 + A的残差 = A的实际值），所以A的残差就是16-15=1（注意，A的预测值是指前面所有树累加的和，这里前面只有一棵树所以直接是15，如果还有树则需要都累加起来作为A的预测值）。进而得到A,B,C,D的残差分别为-1,1，-1,1。然后我们拿残差替代A,B,C,D的原值，到第二棵树去学习，如果我们的预测值和它们的残差相等，则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。这里的数据显然是我可以做的，第二棵树只有两个值1和-1，直接分成两个节点。此时所有人的残差都是0，即每个人都得到了真实的预测值。

 

换句话说，现在A,B,C,D的预测值都和真实年龄一致了。Perfect!：

A: 14岁高一学生，购物较少，经常问学长问题；预测年龄A = 15 – 1 = 14

B: 16岁高三学生；购物较少，经常被学弟问问题；预测年龄B = 15 + 1 = 16

C: 24岁应届毕业生；购物较多，经常问师兄问题；预测年龄C = 25 – 1 = 24

D: 26岁工作两年员工；购物较多，经常被师弟问问题；预测年龄D = 25 + 1 = 26 

 

那么哪里体现了Gradient呢？其实回到第一棵树结束时想一想，无论此时的cost function是什么，是均方差还是均差，只要它以误差作为衡量标准，残差向量(-1, 1, -1, 1)都是它的全局最优方向，这就是Gradient。