ACM 搜索 hdu1016 Prime Ring Problem

  
  
  
  

   
   
   
   Problem Description
  
  
  
  
  
  
  
  

   
   
   
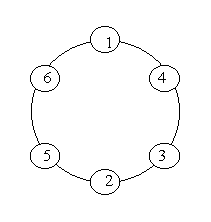
   A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.

Note: the number of first circle should always be 1.


   
   
   
   

  
  
  
  
  
  
  
  

   
   
   
    
  
  
  
  

  
  
  
  

   
   
   
   Input
  
  
  
  
  
  
  
  

   
   
   
   n (0 < n < 20).

  
  
  
  
  
  
  
  

   
   
   
    
  
  
  
  

  
  
  
  

   
   
   
   Output
  
  
  
  
  
  
  
  

   
   
   
   The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.

You are to write a program that completes above process.

Print a blank line after each case.

  
  
  
  
  
  
  
  

   
   
   
    
  
  
  
  

  
  
  
  

   
   
   
   Sample Input
  
  
  
  
  
  
  
  

   
   
   
   
    
    
    
    

     
     
     
     6
8
    
    
    
    
  
  
  
  
  
  
  
  

   
   
   
    
  
  
  
  

  
  
  
  

   
   
   
   Sample Output
  
  
  
  
  
  
  
  

   
   
   
   
    
    
    
    

     
     
     
     Case 1:
1 4 3 2 5 6
1 6 5 2 3 4

Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
    
    
    
    
  
  
  
  

注意：最后一个数要和1检验是否为素数，这是一个环

#include <stdio.h>
 int num[21],mark[21],n; int prime_num[12] = {2,3,5,7,11,13,17,19,23,29,31,37};

//判断是否是质数，是返回1，不是返回0
int is_prime(int a) { for(int i = 0; i < 12;i++) if(a==prime_num[i])return 1; return 0; } void print_num() { for(int i = 1; i < n;i++)
    printf("%d ",num[i]);
    printf("%d",num[n]); } int dfs(int pre,int post,int flag) {
    //如果不符合，直接返回
 if(!is_prime(pre+post)) return 0;
    num[flag] = post; if(flag==n&&is_prime(post+1)) {
        print_num();
        printf("\n"); return 1; }
    //使用过了这个数字就标记为0
    mark[post] = 0; for(int i = 2;i<=n;i++) if(mark[i]!=0 && dfs(post,i,flag+1))break;
    //标记位恢复原状
    mark[post] = 1; return 0; } int main() { int count;
    count = 1; while(scanf("%d",&n)!=EOF) { for(int i = 1; i <= n; i++)
        mark[i] = i;
        num[1] = 1;
        printf("Case %d:\n",count++); if(n==1)printf("1\n"); for(int i = 2;i<=n;i++)
        dfs(1,i,2);
        printf("\n"); } return 0; }