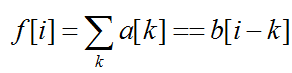BZOJ3160 万径人踪灭 FFT+manacher
对不连续的对称序列计数显然可以转化为对称序列-连续对称序列
连续对称序列显然可以用manacher算法计算得到:P[i]的和即为连续对称序列的个数
所有对称序列总是关于某条对称轴对称,所以对称点的下标和为定值
另f[i]表示以i为对称轴的点对个数(含自身对称)
其中下标为按manacher规则翻倍之后的下标
而这个布尔表达式我处理不来QAQ。。。
膜了PoPoQQQ题解才知道可以强行定下字母之后转为01乘积(这是一种处理01问题的有趣手段)
由于FFT的性质,每对点都会被统计两次(除了自身对称点),实际f[i]=f[i]+1>>1;
注意数组不要开小了。。一定要开够2的XXX次幂才可以。。
#include<cstdio>
#include<complex>
#include<cstring>
#include<iostream>
using namespace std;
typedef long long LL;
const int Mn=300005;
const LL Mod=1000000007;
const double Pi=acos(-1);
int len,n,b[Mn],f[Mn],p[Mn];
char s[Mn],a[Mn];
complex<double>A[Mn],ft[Mn];
LL bin[Mn],ans=0;
void FFT(complex<double>A[],int n,int ty){
int i,j,k,m;
complex<double>t0,t1;
for(i=0;i<n;i++){
for(k=i,j=0,m=1;m<n;m<<=1,j=(j<<1)|(k&1),k>>=1);
if(i<j)t0=A[i],A[i]=A[j],A[j]=t0;
}
ft[0]=1;
for(m=1;m<n;m<<=1){
t0=complex<double>(cos(Pi/m),sin(Pi/m)*ty);
for(j=1;j<m;j++)ft[j]=ft[j-1]*t0;
for(k=0;k<n;k+=(m<<1))
for(i=k;i<k+m;i++){
t0=A[i];t1=A[i+m]*ft[i-k];
A[i]=t0+t1;A[i+m]=t0-t1;
}
}
if(ty==1)return;
for(t0=1.0/n,i=0;i<n;i++)A[i]*=t0;
}
void init(){
int i,j;
scanf("%s",s+1);len=strlen(s+1);
for(n=1;n<(len<<1);n<<=1);
for(i=1;i<=len;i++)b[i]=(s[i]=='a');
for(i=0;i<n;i++)A[i]=b[i];
FFT(A,n,1);
for(i=0;i<n;i++)A[i]*=A[i];
FFT(A,n,-1);
for(i=0;i<n;i++)f[i]+=int(A[i].real()+0.3);
for(i=1;i<=len;i++)b[i]=(s[i]=='b');
for(i=0;i<n;i++)A[i]=b[i];
FFT(A,n,1);
for(i=0;i<n;i++)A[i]*=A[i];
FFT(A,n,-1);
for(i=0;i<n;i++)f[i]+=int(A[i].real()+0.3);
for(bin[0]=i=1;i<=n;i++)bin[i]=bin[i-1]*2%Mod;
for(i=0;i<n;i++)ans=(ans+bin[(f[i]+1)/2]-1)%Mod;
}
void manacher(){
int i,j,k=0,mx=0;
n=0;a[0]='$';
for(i=1;i<=len;i++){
a[++n]='#';a[++n]=s[i];
}
a[n+1]='#';a[n+2]='&';
for(i=0;i<=n;i++){
p[i]=1;
if(mx>i)p[i]=min(mx-i,p[2*k-i]);
while(a[i-p[i]]==a[i+p[i]])p[i]++;
if(i+p[i]>mx){mx=i+p[i];k=i;}
ans=(ans-p[i]/2)%Mod;
}
ans=(ans+Mod)%Mod;
printf("%lld\n",ans);
}
int main(){
init();
manacher();
return 0;
}