LA-3026 - Period-MP算法-失配函数-寻找循环节 （kmp）

大白书上kmp的例题

这里由于没有对失配函数进一步优化，所以叫mp算法。

先用mp算法 得到字符串t 的每一个t[i]的next数组，其中t[i]的next值应该是   （nextval【i+1】） //   失配函数的写法不同而已，也可以改写成t[i]对应next[i]

-----------------------------------------------以上是KMP算法中的失配函数相关内容------------懂了那个失配函数（网上自己学习）再往下看

以下是证明：

-----------------------------------------------------------------------------------------------------------------------------------------------------------

 

-----------------------------------------------------------------------------------------------------------------------------------------------------------
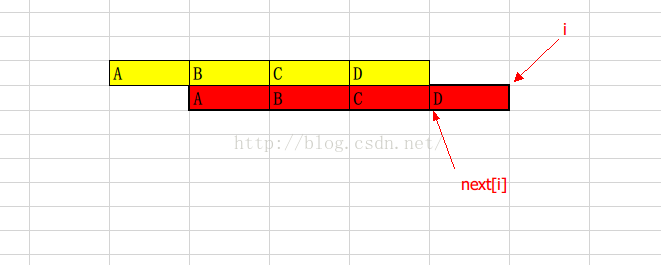
A,B,C,D代表n个不同的数

共4N个数

【1】、从MP算法的失配函数得到 T【i】的next位置为图中下方箭头所指位置   可以确定的是，【0,nex[i]】和【i-next[i],i】是相等的（失配数组的性质），也就是黄色数组的BCD和红色数组的ABC是相等的。

【2】、由于题目要求k大于1，当  i/(i-nex[i]) =2;  即next[i] 为中点;  显然可以分为两段重复的子串，所以k=2。

【3】、当i/(i-next[i])>=2的情况下是否成立呢？  以图为例，可知 i/(i-next[i])=4; 下面我们来看，由【1】得黄色BCD=红色ABC，因为，所以我们可以推知A=B,B=C,C=D,从而A=D； 也就是说，这包含了4个循环节，同理 如果 i/(i-next[i]) = n,那么可以同样地推出  整个串  含有n个循环节。

综上 ，要满足 一个串含有循环节且周期大于1的条件是，i/(i-next[i])==0 (不整除根本凑不了循环节)、 并且由于k>1，所以next[i]!=0，也就是k=1的情况了 。

代码： 

-----------------------------------------------------------------------------------------------------------------------------------------------------------

	#include <cstdio>
	#include <cmath>
	#include <cstring>
	#include <string>
	#include <cstdio>
	#include <algorithm>
	#include <iostream>
	#include <queue>
	#include <set>
	#include <vector>
	#define  inf 0x7fffffff
	#define lson l , m , rt << 1
	#define rson m + 1 , r , rt << 1 | 1
	const int maxn = 1000005;
	using namespace std;
	int nextval[maxn];
	char s[maxn]; 
	int max(int a,int b)
	{return a>b?a:b;}

	void get_next(char *t,int len)	//失配函数

	{
		int i,j;
		i=1; 
		nextval[1]=0;
		j=0;
		while(i<=len)
		{
		
			if (j==0||t[i]==t[j])
			{ 
				j++;
				i++;  

				nextval[i]=j;
				 

				
			}
			else
				j=nextval[j];
		}

	}
 

	int main( )
	{

		int n;
		int cnt=1;
	 while(scanf("%d",&n)!=EOF)
	 {
		 if (!n) break;
		 printf("Test case #%d\n",cnt++);

 		scanf("%s",s+1);
		memset(nextval,0,sizeof(nextval));
 		get_next(s,n);
		int i;
 
		for (i=1;i<=n+1;i++)   //原next数组存的是失配位的下一位 所以本题要减1
		{
			nextval[i]--;
		//	printf("%d ",nextval[i]);
		}
		for (i=1;i<=n;i++)
		{
			
				if ((nextval[i+1])&& ( i%(i-nextval[i+1])==0))
					{
						printf("%d %d\n",i,i/(i-nextval[i+1]));;
					}
				
		} 
		printf("\n");
		
	 }


 

		return 0;
	} 

另一种写法：

#include <cstdio>
#include <cmath>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <map>
#include <set>
#include <vector>
#include <iostream>
using namespace std;

const double pi=acos(-1.0);
double eps=0.000001;

int val[1000005];
char tm[1000005];

void getnext(char *t,int len)
{
	int i,j;
	i=1;
	val[1]=0;
	j=0;
	while(i<len)
	{
		if (j==0||t[i]==t[j])
		{
			i++;j++;val[i]=j;
		}
		else
			j=val[j];
	} 
}

int main()
{
	int cnt=1;
	int n,i;
	while(scanf("%d",&n)!=EOF)
	{
		if (!n)break;
		printf("Test case #%d\n",cnt++);
		scanf("%s",tm+1);
		getnext(tm,n);
		for (i=1;i<=n;i++)
		{
			if (i%(i-val[i])==0&&tm[val[i]]==tm[i])
				if (i/(i-val[i])>1)
				printf("%d %d\n",i,i/(i-val[i]));
			

		}
		printf("\n");
	}
	return 0;
	
} 

-----------------------------------------------------------------------------------------------------------------------------------------------------------