再次理解DFS（POJ1014）

原题目：http://poj.org/problem?id=1014

题目大意：

有分别价值为1,2,3,4,5,6的6种物品，输入6个数字，表示相应价值的物品的数量，问一下能不能将物品分成两份，是两份的总价值相等，其中一个物品不能切开，只能分给其中的某一方，当输入六个0是（即没有物品了），这程序结束，总物品的总个数不超过20000

 

输出：每个测试用例占三行：

          第一行： Collection #k: k为第几组测试用例

          第二行：是否能分（具体形式见用例）

 

一直以为自己已经掌握了DFS。今天遇到POJ1014题目，准备深搜一下。没有用递归，记得老师说过对任何递归算法都能用非递归算法实现。然后就认真地开始写代码，深知动手越快越容易错，我还画了棵树，大概条理了一下深搜的过程。看起来似乎很正确，没有任何问题。可是还是那句老话：除非你用代码将系统实现，并让它动起来，否则你无法真正了解它会有什么问题。按照自己的思路写完之后，开始测试，问题就暴露出来，又少考虑某些情况下需要回溯的问题了。

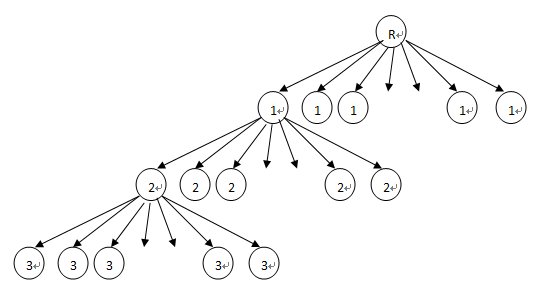
让我们分析如下两图的搜索情况：

一: 没有经过深入思考，我采用了第一种深搜方式，如果sum<halfvalue继续往下探索，如果大于则回溯到上一层，证明上一层选的不合适。认真分析就会发现问题，（1）这个树中的搜索路径很明显不支持同一个数字的若干次选取。（2）仅仅只有六层。这怎么可以呢！照此说不管怎么遍历都是1+2+3+4+5+6.真是汗颜啊怎么写出这么个无厘头的程序呢！

 

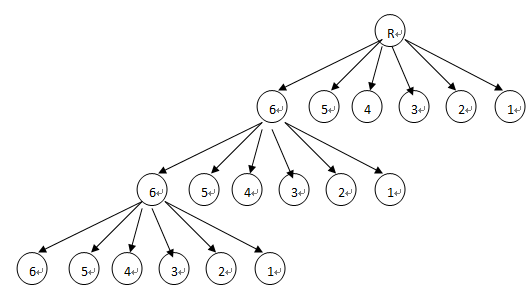
二: 这种搜索是合理的。每次探测都可以有六种选择，也可以想象成从六个盒子里面拿东西，每次从六个盒子里选一种，第一种出现的两种错误都可以避免掉。而且每个节点的度都是6，而且特征一样。这个非常好，对每个节点的处理都一样。很明显可以递归。符合DFS的特点。

附上代码：（借鉴别人的，感觉这段代码写的很精致巧妙啊，让人惭愧啊）

#include<iostream>
using namespace std;

int amount[7] = {0};
int half_value = 0;
int flag = 0;

void DFS(int value, int pre){

	if(value == half_value){
		flag = 1;
		return;
	}

	if(flag == 1){	//不可少的，感受其作用,让递归栈中所有DFS结束
		return;
	}

	int i = 0;
	for(i = pre; i > 0; i--){
		if(amount[i]){
			if(i + value <= half_value){
				amount[i]--;
				DFS(i + value, i);

				if(flag == 1){	//不可少的，感受其作用,让递归栈中所有DFS结束
					return;
				}
			}
		}
	}
}


int main(){

	int testcase = 1;
	while(true){
		flag = 0;
		int totalvalue = 0;
		int N = 6;
		int i = 1;
		while(i <= N){
			cin >> amount[i];
			totalvalue += amount[i] * i;
			i++;
		}

		if(!amount[1] && !amount[2] && !amount[3] && !amount[4] && !amount[5] && !amount[6]){
			break;
		}

		printf("Collection #%d:\n", testcase++);
		if(totalvalue % 2 != 0){
			cout << "Can't be divided." << endl << endl;
			continue;
		}

		half_value = totalvalue / 2;
		DFS(0, 6);		

		if(flag){
			cout << "Can be divided." << endl;
		} else {
			cout << "Can't be divided." << endl;
		}
		cout << endl;
	}	
	return 0;
}