稀疏矩阵的存储格式(Sparse Matrix Formats)
稀疏矩阵的存储格式(Sparse Matrix Storage Formats)
1.Coordinate Format(COO)
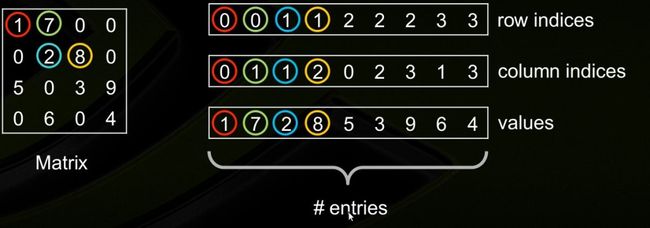
这种存储方式的主要优点是灵活、简单。仅存储非零元素以及每个非零元素的坐标。
使用3个数组进行存储:values, rows, andcolumn
values: 实数或复数数据,包括矩阵中的非零元素, 顺序任意。
rows: 数据所处的行。
columns: 数据所处的列.
参数:矩阵中非零元素的数量 nnz,3个数组的长度均为nnz.
import numpy as np
from scipy.sparse import coo_matrix
coo_matrix((3, 4), dtype=np.int8).toarray()
array([[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]], dtype=int8)
row = np.array([0, 3, 1, 0])
col = np.array([0, 3, 1, 2])
data = np.array([4, 5, 7, 9])
coo_matrix((data, (row, col)), shape=(4, 4)).toarray()
array([[4, 0, 9, 0], [0, 7, 0, 0], [0, 0, 0, 0], [0, 0, 0, 5]])
# example with duplicates
row = np.array([0, 0, 1, 3, 1, 0, 0])
col = np.array([0, 2, 1, 3, 1, 0, 0])
data = np.array([1, 1, 1, 1, 1, 1, 1])
coo_matrix((data, (row, col)), shape=(4, 4)).toarray()
array([[3, 0, 1, 0], [0, 2, 0, 0], [0, 0, 0, 0], [0, 0, 0, 1]])2.Diagonal Storage Format (DIA,对角线存储格式?不太懂)
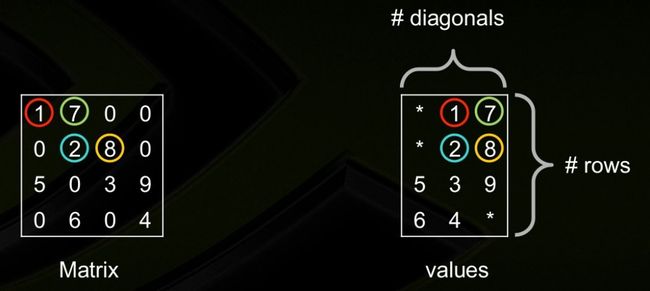
The Intel MKL diagonal storage format is specified by two arrays:values and distance, and two parameters:ndiag, which is the number of non-empty diagonals(非零对角线), and lval, which is the declared leading dimension in the calling (sub)programs.
from scipy.sparse import dia_matrix
dia_matrix((3, 4), dtype=np.int8).toarray()
array([[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]], dtype=int8)
data = np.array([[1, 2, 3, 4]]).repeat(3, axis=0)
offsets = np.array([0, -1, 2])
dia_matrix((data, offsets), shape=(4, 4)).toarray()
#where the data[k,:] stores the diagonal entries for diagonal offsets[k]
array([[1, 0, 3, 0], [1, 2, 0, 4], [0, 2, 3, 0], [0, 0, 3, 4]])
3.Compressed Sparse Row Format (CSR)
from scipy.sparse import csr_matrix
csr_matrix((3, 4), dtype=np.int8).toarray()
array([[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]], dtype=int8)
row = np.array([0, 0, 1, 2, 2, 2])
col = np.array([0, 2, 2, 0, 1, 2])
data = np.array([1, 2, 3, 4, 5, 6])
csr_matrix((data, (row, col)), shape=(3, 3)).toarray()
array([[1, 0, 2], [0, 0, 3], [4, 5, 6]])
indptr = np.array([0, 2, 3, 6])# 为什么要有4个元素??每个元素代表一行,其数值代表该行从indices中哪个元素开始.indices是列号
indices = np.array([0, 2, 2, 0, 1, 2])
data = np.array([1, 2, 3, 4, 5, 6])
csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2], [0, 0, 3], [4, 5, 6]])
As an example of how to construct a CSR matrix incrementally, the following snippet builds a term-document matrix from texts:
docs = [["hello", "world", "hello"], ["goodbye", "cruel", "world"]]
indptr = [0]
indices = []
data = []
vocabulary = {}
for d in docs:
for term in d:
index = vocabulary.setdefault(term, len(vocabulary))
indices.append(index)
data.append(1)
indptr.append(len(indices))
csr_matrix((data, indices, indptr), dtype=int).toarray()
array([[2, 1, 0, 0], [0, 1, 1, 1]])4.Compressed Sparse Column Format (CSC)
和CSR差不多。
The compressed sparse column format (CSC) is similar to the CSR format, but the columns are used instead the rows. In other words, the CSC format is identical to the CSR format for the transposed matrix. The CSR format is specified by four arrays: values, columns, pointerB, and pointerE. The following table describes the arrays in terms of the values, row, and column positions of the non-zero elements in a sparse matrixA.
values
A real or complex array that contains the non-zero elements ofA. Values of the non-zero elements ofA are mapped into thevalues array using the column-major storage mapping.
rows
Element i of the integer array rows is the number of the row inA that contains thei-th value in thevalues array.
pointerB
Element j of this integer array gives the index of the element in thevalues array that is first non-zero element in a columnj ofA. Note that this index is equal topointerB(j) -pointerB(1)+1 .
pointerE
An integer array that contains column indices, such thatpointerE(j)-pointerB(1) is the index of the element in thevalues array that is last non-zero element in a column j ofA.
5. Skyline Storage Format
6. Block Compressed Sparse Row Format (BSR)
from scipy.sparse import bsr_matrix
bsr_matrix((3, 4), dtype=np.int8).toarray()
array([[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]], dtype=int8)
row = np.array([0, 0, 1, 2, 2, 2])
col = np.array([0, 2, 2, 0, 1, 2])
data = np.array([1, 2, 3 ,4, 5, 6])
bsr_matrix((data, (row, col)), shape=(3, 3)).toarray()
array([[1, 0, 2], [0, 0, 3], [4, 5, 6]])
indptr = np.array([0, 2, 3, 6])
indices = np.array([0, 2, 2, 0, 1, 2])
data = np.array([1, 2, 3, 4, 5, 6]).repeat(4).reshape(6, 2, 2)
bsr_matrix((data,indices,indptr), shape=(6, 6)).toarray()
array([[1, 1, 0, 0, 2, 2], [1, 1, 0, 0, 2, 2], [0, 0, 0, 0, 3, 3], [0, 0, 0, 0, 3, 3], [4, 4, 5, 5, 6, 6], [4, 4, 5, 5, 6, 6]])bsr_matrix((data, indices, indptr), [shape=(M, N)])
is the standard BSR representation where the block column indices for row i are stored in indices[indptr[i]:indptr[i+1]] and their corresponding block values are stored in data[ indptr[i]: indptr[i+1] ]. If the shape parameter is not supplied, the matrix dimensions are inferred from the index arrays.
