算法之道（一）（未完，待续）
这几天一直捉摸着怎么能有一个完善的计划，和整理文档、整理知识的方式，因为我想既然我一个人有这种感觉，那么肯定有很多的人和我一样有着这种马上行动的想法。互联网是一个大家庭，我们在这里学习，同时为什么我们能学习，因为前人给了我们资料，所以我们更应该学会分享。
——学习如逆水行舟，不进则退！
最近准备好好的花一些时间彻底的整理一下网络上的资源，一些分门别类的笔试题，算法题，单凭百度、Google这样的搜索引擎，抑或者是IT面试社区（http://www.itmian4.com）、csdn技术社区(http://www.csdn.net)等等这样的技术性社区，可能是减少了我们的查找范围，可是毕竟它们的面向用户还是非常非常的广泛，我一直有一个想法，我们必须有自己的分享渠道，具体满足同一特征的人群的需求。
可能最近还没什么非常完善的计划或者措施，但是会把我学习中查阅的，真正可用性高的东西整理制作成pdf文档分享给大家，时间现在还不确定。呵呵~~~
好了，言归正传，今天要分享的是几道偏算法的笔试题，都是真题喔。
可能题目不是很难，对于有些人说会有点简单，但是简单的题目也会有不同的解法，抱着交流和追求完美的心态，看看这几个题目：
1、这是一道2013年9-10月份，阿里的2014校招研发工程师笔试的一道大题。
题目如下：有一个算法，查找n个元素的的数组的最大值和最小值，要比较2n次；请写一个最高效的算法，并说明他要比较的次数。
(请注意复杂度的常数部分，不用写代码，说明步骤和过程即可，要定出比较的次数，没写不给分)
分析：这道题目难度不是很大，可能有好几种解法。今年博主去参加完笔试，出来之后无不是听身边的人说如何如何简单，不知道是不是真的如此。阿里莫非是放宽了笔试的限制，而想在大范围的面试环节筛选精英。对于这个我不得而知了。
题目说的很清楚，寻找一个数组中的最大值和最小值，并说其中已经有一个算法，在复杂度为2n的情况下就能完成任务。并且提示了一句，要注意复杂度的的常数部分，我当时就被这坑爹的一句话给带错了方向。因为我心里一看到这道题就有个方法：设置一个max和min，初始时都为数组下标为0的元素那个值，然后依次往后遍历整个数组，每次都把当前元素和max比较，如果比max大，则max赋值为当前元素的值，如果比max小，则与min比较，如果比min的值小，则min赋值为当前元素的值，直到遍历完整个数组。
这样完成下来，算最糟糕的情况，比较次数是遍历的次数（N-1）加上每次遍历最多比较2次，最终总共是比较了2N-2次。看到没，2N-2，是不是比题目中的2N多了一个负数的常数。我就没再深究，就这样赤裸裸的、赤裸裸的……看下一道题目去了。阿里，你赔我的offer！！！可伤心了。
因为把笔试的试卷偷偷携带出了考场，回来之后又好好的认认真真的看了一遍题目，敲了几行代码，于是恍然大惊，现给出新解法如下：
将数组中的元素进行分组，从下标0开始，两两为一组，每组中的两个数互相比较，得到较大者和较小者，默认第一组（也就是下标为0和1的元素）中较大者为max，较小者为min，依次拿max与之后每一组的较大者，拿min与之后每一组的较小者比较。最终得到的max和min即为数组中的最大值和最小值。* [注意：当数组长度为奇数时，必有最后一个元素没有被分到任何组中，需要在最后比较。]
算法复杂度：
当数组长度为偶数时，考虑最糟糕的情况，分为N/2个组，每组的2个元素互相比较一次，然后第一组的较大者和较小者分别与之后每一组的较大者和较小者比较，总共N/2+(N/2-1)*2 = 3N/2-2次！
当数组长度为奇数时，考虑最糟糕的情况，分为N/2个组加1个单独的元素，前面的情况同上，最后还要多比较2次，总共3N/2-2+2 = 3N/2次！
public class FindNumberSort{
/**
* 题目：根据传入的整型数组，找出其中最大和最小的元素
* 要求：算法复杂度小于2N
*
* 解题思路：将数组中的元素进行分组，从下标0开始，两两为一组，每组中的两个数互相比较，
* 得到较大者和较小者，默认第一组（也就是下标为0和1的元素）中较大者为max，较小者为min
* ，依次拿max与之后每一组的较大者，拿min与之后每一组的较小者比较。
* 最终得到的max和min即为数组中的最大值和最小值。
* [注意：当数组长度为奇数时，必有最后一个元素没有被分到任何组中，需要在最后比较。]
*
* 算法复杂度：
* 当数组长度为偶数时，考虑最糟糕的情况，分为N/2个组，每组的2个元素互相比较一次，
* 然后第一组的较大者和较小者分别与之后每一组的较大者和较小者比较，
* 总共N/2+(N/2-1)*2 = 3N/2-2次！
* 当数组长度为奇数时，考虑最糟糕的情况，分为N/2个组加1个单独的元素，前面的情况同上，
* 最后还要多比较2次，总共3N/2-2+2 = 3N/2次！
*
* 作者:疯子
* 创建时间：2013.12.28
* CSDN博客地址：http://blog.csdn.net/limenglin0927
*/
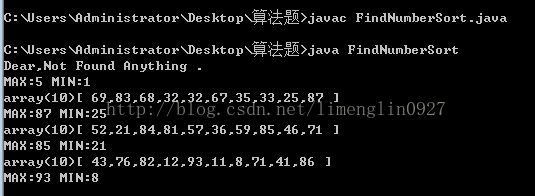
public static void findMaxAndMinNumber(int[] arr) {
int length = arr.length;
if(arr==null || length<1) {
System.out.println("Dear,Not Found Anything .");
return;
} else if(length == 1){
System.out.println("Dear,Only One Suger.it is number[ "+arr[0]+" ]");
} else {
//初始化
int max = arr[0];
int min = arr[1];
if(max<min) {
max = arr[1];
min = arr[0];
}
//循环所有分组，i为分组第一个元素下标，j为分组第二个元素下标
for(int i=2,j=3; i<length && j<length; i=i+2,j=j+2){
int amax = -1;
int amin = -1;
if(arr[i]>arr[j]){
if(arr[i] > max){
max = arr[i];
}
if(arr[j] < min){
min = arr[j];
}
} else {
if(arr[j] > max) {
max = arr[j];
}
if(arr[i] < min) {
min = arr[i];
}
}
}
//所有组比较一遍过后，要考虑当数组长度为奇数时最后一个数未分组的情况
if(length%2 != 0){
if(arr[length-1] > max) {
max = arr[length-1];
} else if(arr[length] < min) {
min = arr[length];
}
}
//结果
System.out.println("MAX:"max+" MIN:"+min);
}
}
/**
* 打印整型数组
*/
public static void printIntArray(int[] arr) {
StringBuffer sb = new StringBuffer();
sb.append("array("+arr.length+")[ ");
for(int i=0;i<arr.length;i++){
sb.append(arr[i]+",");
}
if(sb.length()>0 && sb.charAt(sb.length()-1)==',') {
sb = sb.deleteCharAt(sb.length()-1);
}
sb.append(" ]");
System.out.println(sb.toString());
}
/**
* 测试的main方法
*/
public static void main(String[] args) {
int[] arr1 = null;
findMaxAndMinNumber(arr1) ;
int[] arr2 = {1,2,3,4,5};
findMaxAndMinNumber(arr2) ;
int[] arr3 = new int[10];
for(int count=0;count<3;count++) { //随机测试3次
//初始化
for(int i=0;i<arr.length;i++){
arr[i] = (int)(Math.random()*100);//随机获得10个小于100的整数
}
printIntArray(arrt);
findMaxAndMinNumber(arrt) ;
}
}
}
—————————
这道题，还想过一种解法，就是因为java语言中，容器类中的Set就是带排序功能的，那么只需要把数组构建成一个Set类型的对象就可以了。时间复杂度貌似是 N 啊。
如果哪位大虾，还有更好的解法，欢迎分享！或者你有什么不明白的地方，都可以在下面评论中写出。我会经常关注回复的，谢谢！！！
2、这是一道百度2014校园招聘深度学习算法研发工程师的笔试题。
题目如下：有这样一个数组A,大小为n，相邻元素差的绝对值都是1，如A={4,5,6,5,6,7,8,9,10,9}。现在给定数组A和目标整数t，请找到t在数组中的位置。(15分)
分析：这道题目刚拿到手上，我第一个想到的就是边界问题，等下写程序的时候一定要考虑找不到t和找到多个t的情况。有点强迫症了都，貌似优秀的程序员都是或多或少都是追求完美的。（纯属自我安慰）。最简单的方法便是遍历整个数组，就能找到所有存在之中的t，算法复杂度为N，这个可能大家都知道。可是这个数组中的元素有一个非常突出且明告诉你的特征，所有相邻元素差的绝对值为1，也就是相邻的元素只能加1，或者减1。
我想到的解法如下：从数组第一个元素开始，实行跳跃式的搜索。怎么跳跃呢？将当前元素和t进行比较，设当前元素下标为i，如果| t-arr[i] |的值为0，则表示找到元素t，则下次搜索的目标元素下标则为i+2，如果差的绝对值不为0，则下次搜索的目标元素下标为i+|t-arr[i]|，也就是向前跳跃差的绝对值个元素进行搜索。直到遍历完整个数组。
以A={4,5,6,5,6,7,8,9,10,9}，t=6为例子，首先i=0，6-4的绝对值为2，就可以直接跳跃2步搜索i=2,应为就算一直递增，也只能在2步之后到达6，所以中间的完全没有可能。然后发现i=2时，发现6-6的绝对值为0，即找到结果，然后继续遍历，并且i=i+2，这时候的跳步搜索 是因为 只有+1再-1至少两步之后才能再次相等。大概原理就是这样。
public class FindNumSort{
/**
* 题目：有这样一个数组A,大小为n，相邻元素差的绝对值都是1，如A={4,5,6,5,6,7,8,9,10,9}
* 现在给定数组A和目标整数t，请找到t在数组中的位置。
* 要求：算法复杂度越小越好，小于N
*
* 作者:疯子
* 创建时间：2013.12.28
* CSDN博客地址：http://blog.csdn.net/limenglin0927
*/
public static void findTNumber(int[] arr, int t) {
int length = arr.length;
if(arr==null || length<1) {
System.out.println("Dear, Not Found Anything .");
return;
} else {
int count = 0;
for(int i=0;i<length;){
int abs = Math.abs(t-arr[i]);
if(abs==0) {
System.out.println("Found Number:"+t+" ,Index:"+i);
count++;
i = i+2;
} else {
i = i+abs;
}
}
if(count>0) {
System.out.println("Not Found Number "+t+" In The Array");
} else {
System.out.println("That Found All "+count+" Datas");
}
}
}
/**
* 打印整型数组
*/
public static void printIntArray(int[] arr) {
StringBuffer sb = new StringBuffer();
sb.append("array("+arr.length+")[ ");
for(int i=0;i<arr.length;i++){
sb.append(arr[i]+",");
}
if(sb.length()>0 && sb.charAt(sb.length()-1)==',') {
sb = sb.deleteCharAt(sb.length()-1);
}
sb.append(" ]");
System.out.println(sb.toString());
}
/**
* 测试的main方法
*/
public static void main(String[] args) {
int[] arr = {4,5,6,5,6,7,8,9,10,9};
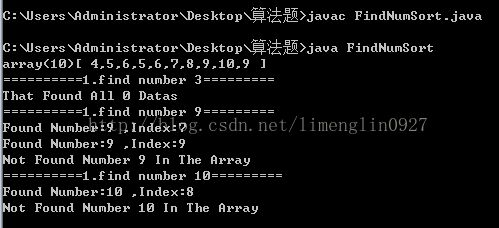
printIntArray(arr);
System.out.println("==========1.find number 3=========");
findTNumber(arr,3);
System.out.println("==========1.find number 9=========");
findTNumber(arr,9);
System.out.println("==========1.find number 10=========");
findTNumber(arr,10);
}
}
3、这是阿里巴巴2013年10月份的2014校招研发工程师的笔试题
题目如下：有三个非递减序列的数组a[l]、b[m]、c[n]，求他们之间的最小距离。已知距离的定义如下：
distance = max(|a[i]-b[j]|, |a[i]-c[]k|, |b[j]-c[k]|).其中0<=i<l, 0<=j<m, 0<=k<n。
未完，待续。。。。。