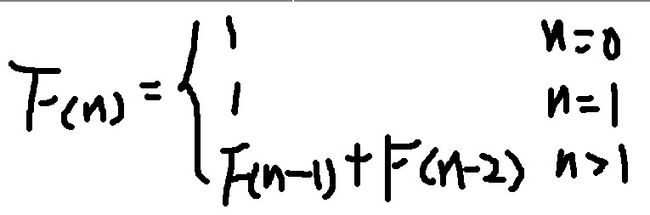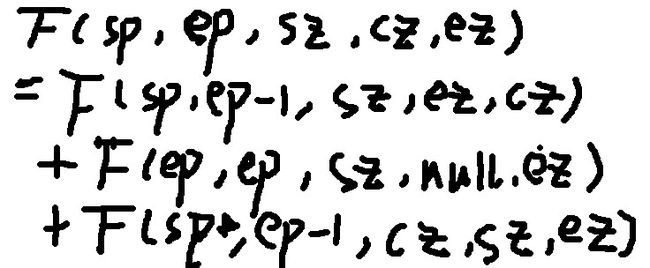梦之递归分治法
题解
1, 递归分治法
分治法的设计思想是:将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
三个步骤:
step1 分解:将原问题分解为若干个规模较小,相互独立,与原问题形式相同的子问题;
step2 解决:若子问题规模较小而容易被解决则直接解,否则递归地解各个子问题
step3 合并:将各个子问题的解合并为原问题的解。
No1:斐波那契数列(Fibonacci数列)
问题描述:一个数列,当n=0或1时,F(n)=1;当n>1时,F(n)=F(n-1)+F(n-2);示例如:1、1、2、3、5、8、13……
问题分析:这是一个可以用简单的递归方程式解决的问题。通过这个数列的规律,即可马上得到这个数列的递归关系式,我们先定义F(n)为该数列中下标为n的那个数的值。
图1-1
显而易见地可以看出该数列存在的原问题的子问题。当自变量为某一个值时,所求结果能为一个固定数值,则可看做一个递归的出口,当自变量为某一值时,结果为由比原问题更简单的子问题组成,并且子问题的性质与原问题相同,只是规模更小,在此递归求解。最后程序到达出口处完成输出即为原问题的解。
参考答案:原问题F(n)为斐波那契数列的第n个数的值;
子问题为当n>1时,F(n)=F(n-1)+F(n-2);
当n=0或1时,F(n)=1。
递归出口为F(0)=F(1)=1。
注意:(最好给出递归关系式,就是上图1-1那种形式的方程式。然后三要素:原问题用什么表示、子问题的划分、最后要给出函数终止的条件)
No2:汉诺塔问题
问题描述:从1到n编号的盘子,其编号越大则盘子的大小越大。有三根柱子A,B,C,盘子能放在柱子上,并且只能是小盘子放在大盘子之上。汉诺塔问题正是求解如何将n个盘子从A柱借助B柱子移动到C柱。
问题分析:这是一个典型的适用递归描述的问题。通过分析,我们可以知道,原问题可以描述为F(start_panzi,end_panzi,start_zhuzi, center_zhuzi, end_zhuzi),翻译为:
F(最小的盘号,最大的盘号,原先所在的柱子,能够借助的柱子,最终要移动到的柱子)
如F(1,3,A,B,C)为把从1号到3号盘子,从A柱借助B柱移到C柱。
我们能够发现现在我们就能把原问题划分成3个步骤完成,先把从1到n-1个盘子从A借助C移动到B,再把第n个盘子直接移动到C,最后把从1到n-1个盘子从B借助A移动到C即可。
图1-2
参考答案:原问题F(sp,ep,sz,cz,ez)为将编号从sp到ep的所有盘子从sz柱,借助cz柱,移动到ez柱。
子问题为将原问题划分为3个步骤来完成:第一步将最后一个盘子不动,即将sp到ep-1号的盘子从sz柱借助ez暂时放到cz中间柱,再把第ep个盘子直接从sz放到ez柱上去,最后再把放在中间柱cz上的sp到ep-1盘从cz借助sz移动到ez就完成了。
递归出口为当问题中只有一个盘子的时候就只需要将该盘从所在柱子直接放到目标柱子(即子问题拆分的第2步)。
注:最好写出上图1-2中的递归关系式。
总结:解决递归问题,只需分析得出原问题+子问题+递归出口。如果在能写出递归关系式的情况下,尽量给出,递归关系式能言简意赅的让别人明白拆分步骤,而且能直接简单的转换为相对应的代码。
附1:二分搜索问题
参考答案:原问题为Search(low,high,num)在已排序的数组下标为low到high之间寻找num元素。默认为从小到大的有序数组。
子问题划分为首先取low到high最中间的那个元素,即下标为center=(low+high)/2的元素记为mmp,如果等于num则返回表示已找到,如果mmp<num则向右区间搜索(center+1到high之间),如果mmp>num则向左区间搜索(low到center-1之间)。
递归出口为mmp==num的时候表示已找到,则正常退出。还有当遍历整个数组还没有找到则退出,表示该数组中并没有num这个数。
递归关系式:图1-3