poj1419 Graph Coloring
Graph Coloring
| Time Limit: 1000MS | Memory Limit: 10000K | |||
Description
You are to write a program that tries to find an optimal coloring for a given graph. Colors are applied to the nodes of the graph and the only available colors are black and white. The coloring of the graph is called optimal if a maximum of nodes is black. The coloring is restricted by the rule that no two connected nodes may be black.
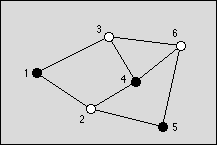
Figure 1: An optimal graph with three black nodes

Figure 1: An optimal graph with three black nodes
Input
The graph is given as a set of nodes denoted by numbers 1...n, n <= 100, and a set of undirected edges denoted by pairs of node numbers (n1, n2), n1 != n2. The input file contains m graphs. The number m is given on the first line. The first line of each graph contains n and k, the number of nodes and the number of edges, respectively. The following k lines contain the edges given by a pair of node numbers, which are separated by a space.
Output
The output should consists of 2m lines, two lines for each graph found in the input file. The first line of should contain the maximum number of nodes that can be colored black in the graph. The second line should contain one possible optimal coloring. It is given by the list of black nodes, separated by a blank.
Sample Input
1 6 8 1 2 1 3 2 4 2 5 3 4 3 6 4 6 5 6
Sample Output
3 1 4 5
Source
Southwestern European Regional Contest 1995
求最大点独立集,建反图,求最大团
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <cmath>
#include <ctime>
#include <vector>
#include <cstdio>
#include <cctype>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
using namespace std;
#define INF 0x3f3f3f3f
#define inf -0x3f3f3f3f
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define mem0(a) memset(a,0,sizeof(a))
#define mem1(a) memset(a,-1,sizeof(a))
#define mem(a, b) memset(a, b, sizeof(a))
#define Hash(a,b) (a-1)*n+b
typedef long long ll;
const int maxn=121;
int num[maxn];
int G[maxn][maxn],ret,pre[maxn];
set<int>st[maxn];
bool dfs(int fa,int pre,int *adj,int tot,int cnt){
if(tot==0){
if(cnt>ret){
ret=cnt;
st[fa].insert(pre);
return 1;
}
return 0;
}
for(int i=0;i<tot;i++){
if(cnt+tot-i<=ret)
continue;
if(cnt+num[adj[i]]<=ret)
continue;
int t[maxn],k=0;
for(int j=i+1;j<tot;j++){
if(G[adj[i]][adj[j]])
t[k ++] = adj[j];
}
if(dfs(fa,adj[i],t,k,cnt+1)){
st[fa].insert(pre);
return 1;
}
}
return 0;
}
void Maxclique(int n){
int adj[maxn],tot;
for(int i=n;i>=1;i--){
tot=0;
for(int j=i+1;j<=n;j++)
if(G[i][j]==1)
adj[tot++]=j;
int ans=ret;
dfs(i,i,adj,tot,1);
num[i]=ret;
}
}
int main(){
int _;
int n,m;
scanf("%d",&_);
while(_--){
scanf("%d%d",&n,&m);
mem0(G);
mem1(pre);
for(int i=1;i<=n;i++)
st[i].clear();
ret=0;
int u,v;
for(int i=1;i<=m;i++){
scanf("%d%d",&u,&v);
G[u][v]=G[v][u]=1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
if(i!=j)
G[i][j]^=1;
}
Maxclique(n);
printf("%d\n",ret);
for(int i=1;i<=n;i++)
if(st[i].size()==ret){
u=i;
break;
}
set<int>::iterator it;
it=st[u].begin();
printf("%d",*it);
it++;
while(it!=st[u].end()){
printf(" %d",*it);
it++;
}
printf("\n");
}
return 0;
}