hdu 4328 (悬线法+dp)
悬线法用于求解最大子矩阵问题,资料详见:这篇论文
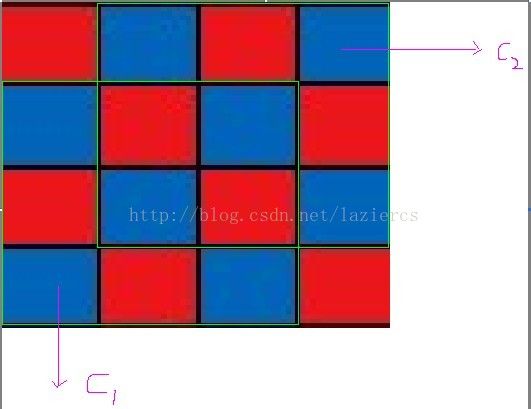
对于red-and-blue crisscross 方阵可以用dp,既可以用合并两个小方阵得到一个大方阵,合并过程如下图:
我们可以把两个绿色的3*3小方阵合成一个4*4大方阵,只要符合color[i][j]!=color[i-1][j]&&color[i][j]!=color[i][j-1]&&color[i][j]==color[i-k][j-k]( k为min(dp[i-1][j],dp[i][j-1]));
dp[i][j]表示正方形的右下坐标为(i,j)的最大方阵的边长;
#include<stdio.h>
#include<string.h>
#define N 1100
int H[N][N],right[N][N],left[N][N],mat[N][N],n,m;
void init()
{
int i,j,b;
for(i=1;i<=n;i++){
for(j=1,b=0;j<=m;j++){
if(!mat[i][j]) b=0;
else if(!b&&mat[i][j]) b=j;
left[i][j]=b;
}
for(j=m,b=0;j>=1;j--){
if(!mat[i][j]) b=0;
else if(!b&&mat[i][j]) b=j;
right[i][j]=b;
}
}
}
int max(int a,int b){ return a<b?b:a; }
int min(int a,int b){ return a>b?b:a; }
int solve()
{
int i,j,ans=0;
memset(H,0,sizeof(H));
for(i=1;i<=n;i++){
for(j=1;j<=m;j++)
{
if(mat[i][j]){
H[i][j]=H[i-1][j]+1;
if(mat[i-1][j])
{
left[i][j]=max(left[i][j],left[i-1][j]);
right[i][j]=min(right[i][j],right[i-1][j]);
}
ans=max(ans,2*(right[i][j]-left[i][j]+1)+2*H[i][j]);
}
}
}
return ans;
}
char in[N][N];
void input()
{
int i,j;
scanf("%d%d",&n,&m);
for(i=1;i<=n;i++) scanf("%s",in[i]+1);
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
mat[i][j]=in[i][j]=='R';
}
int dp[N][N];
int intersect()
{
int i,j,k,ans=0;
memset(dp,0,sizeof(dp));
for(i=1;i<=n;i++)
{
for(j=1;j<=m;j++)
{
dp[i][j]=1;
if(mat[i-1][j]!=mat[i][j]&&mat[i][j]!=mat[i][j-1]){
k=min(dp[i-1][j],dp[i][j-1]);
if(mat[i][j]==mat[i-k][j-k])k++;
dp[i][j]=max(dp[i][j],k);
ans=max(ans,dp[i][j]*4);
}
}
}
return ans;
}
int main()
{
int ans,i,j,cas,cass;
scanf("%d",&cass);
for(cas=1;cas<=cass;cas++)
{
input();
ans=intersect();
init();
ans=max(ans,solve());
for(i=1;i<=n;i++) for(j=1;j<=m;j++) mat[i][j]=1-mat[i][j];
init();
ans=max(ans,solve());
printf("Case #%d: %d\n",cas,ans);
}
return 0;
}