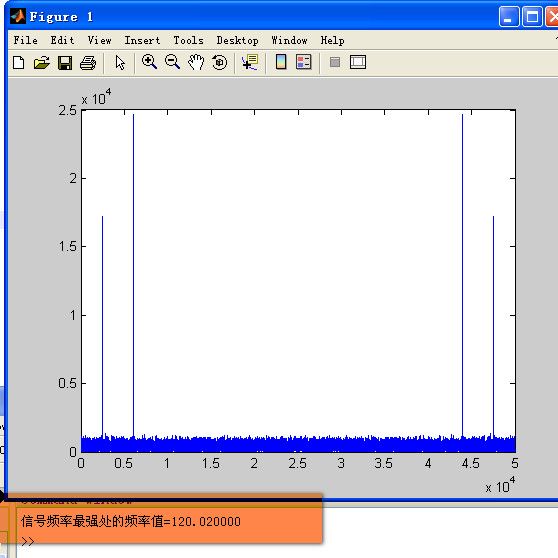
用matlab寻找一个信号中频率最强最大的哪一点位置

1. 产生一个50和120Hz的信号，并叠加上了一些噪声；

2. 采样频率为1KHz，远远大于信号频率，当然能取出50和120Hz两个值；

3. 经默认函数fft变换后（不带点数N），返回一个和时域信号相同大小个数的数组Z；

4. fft函数后，返回数组Z的个数值，正好对应采样频率的范围，因此查找Z的最值，和对应的下标，就能对应上最值的频率：

clear; close all; clc;
Fs = 1000;           %采样率
T = 1/Fs;                     
L = 50000;           % 信号持续的时间
t = (0:L-1)*T;                
x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); % 产生一个信号
y = x + 2*randn(size(t));     % 叠加上噪声
plot(Fs*t(1:50),y(1:50))
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('time (milliseconds)')
Y = fft(y);
Z=abs(Y);
plot(Z) 
[ma, I]=max(Z);	%ma为数组的最大值，I为下标值
fprintf(1, '信号频率最强处的频率值=%f\n', I/length(Z)*Fs);

可以试验，改变上述的采样频率fs值，信号持续时间L，不会最后的输出结果。

如果，fft函数使用了第二个参数“FFT点数N”，那么该函数返回的大小为N，fs和N的范围一一对应，如下程序：

clear; close all; clc;
Fs = 6000;           %采样率
T = 1/Fs;                     
L = 50000;           % 信号持续的时间
t = (0:L-1)*T;                
x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); % 产生一个信号
y = x + 2*randn(size(t));     % 叠加上噪声
plot(Fs*t(1:50),y(1:50))
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('time (milliseconds)')

N=4096*4;		%随便写，只要基为2得到即可
Y = fft(y, N);

Z=abs(Y);
plot(Z) 
[ma, I]=max(Z);	%ma为数组的最大值，I为下标值
fprintf(1, '信号频率最强处的频率值=%f\n', I/length(Z)*Fs);