蓝桥杯 MST 和 搜索

链接：戳这里

  历届试题 兰顿蚂蚁  

时间限制：1.0s   内存限制：256.0MB

    

问题描述

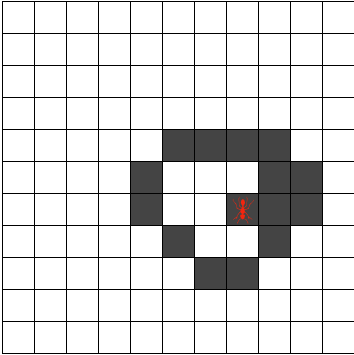
　　兰顿蚂蚁，是于1986年，由克里斯·兰顿提出来的，属于细胞自动机的一种。

　　平面上的正方形格子被填上黑色或白色。在其中一格正方形内有一只“蚂蚁”。
　　蚂蚁的头部朝向为：上下左右其中一方。

　　蚂蚁的移动规则十分简单：
　　若蚂蚁在黑格，右转90度，将该格改为白格，并向前移一格；
　　若蚂蚁在白格，左转90度，将该格改为黑格，并向前移一格。

　　规则虽然简单，蚂蚁的行为却十分复杂。刚刚开始时留下的路线都会有接近对称，像是会重复，但不论起始状态如何，蚂蚁经过漫长的混乱活动后，会开辟出一条规则的“高速公路”。

　　蚂蚁的路线是很难事先预测的。

　　你的任务是根据初始状态，用计算机模拟兰顿蚂蚁在第n步行走后所处的位置。

输入格式

　　输入数据的第一行是 m n 两个整数（3 < m, n < 100），表示正方形格子的行数和列数。
　　接下来是 m 行数据。
　　每行数据为 n 个被空格分开的数字。0 表示白格，1 表示黑格。

　　接下来是一行数据：x y s k, 其中x y为整数，表示蚂蚁所在行号和列号（行号从上到下增长，列号从左到右增长，都是从0开始编号）。s 是一个大写字母，表示蚂蚁头的朝向，我们约定：上下左右分别用：UDLR表示。k 表示蚂蚁走的步数。

输出格式

　　输出数据为两个空格分开的整数 p q, 分别表示蚂蚁在k步后，所处格子的行号和列号。

样例输入

5 6
0 0 0 0 0 0
0 0 0 0 0 0
0 0 1 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
2 3 L 5

样例输出

1 3

样例输入

3 3
0 0 0
1 1 1
1 1 1
1 1 U 6

样例输出

0 0

思路：莫名其妙教练报的蓝桥杯  估计会GG

代码：

#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[110][110];
struct node{
	int x,y;
	char c;
	node(){}
	node(int x,int y,char c):x(x),y(y),c(c){}
};
queue<node> qu;
int main(){
	scanf("%d%d",&n,&m);
	for(int i=0;i<n;i++){
		for(int j=0;j<m;j++){
			scanf("%d",&a[i][j]);
		}
	}
	int x,y,k;
	char c[2];
	scanf("%d%d%s%d",&x,&y,&c,&k);
	node tmp;
	tmp.x=x;tmp.y=y;tmp.c=c[0];
	qu.push(tmp);
	while(!qu.empty()){
		node next,now=qu.front();
		qu.pop();
		///printf("k=%d %d %d %c\n",k,now.x,now.y,now.c);
		if(k) k--;
		else {
			printf("%d %d\n",now.x,now.y);
			return 0;
		}
		if(now.c=='L'){
			if(a[now.x][now.y]==0){
				next.x=now.x+1;
				next.y=now.y;
				next.c='D';
				a[now.x][now.y]=1;
				qu.push(next);
			} else{
				next.x=now.x-1;
				next.y=now.y;
				next.c='U';
				a[now.x][now.y]=0;
				qu.push(next);
			}
		} else if(now.c=='R'){
			if(a[now.x][now.y]==0){
				next.x=now.x-1;
				next.y=now.y;
				next.c='U';
				a[now.x][now.y]=1;
				qu.push(next);
			} else {
				next.x=now.x+1;
				next.y=now.y;
				next.c='D';
				a[now.x][now.y]=0;
				qu.push(next);
			}
		} else if(now.c=='U'){
			if(a[now.x][now.y]==0){
				next.x=now.x;
				next.y=now.y-1;
				next.c='L';
				a[now.x][now.y]=1;
				qu.push(next);
			} else {
				next.x=now.x;
				next.y=now.y+1;
				next.c='R';
				a[now.x][now.y]=0;
				qu.push(next);
			}
		} else if(now.c=='D'){
			if(a[now.x][now.y]==0){
				next.x=now.x;
				next.y=now.y+1;
				next.c='R';
				a[now.x][now.y]=1;
				qu.push(next);
			} else {
				next.x=now.x;
				next.y=now.y-1;
				next.c='L';
				a[now.x][now.y]=0;
				qu.push(next);
			}
		}
	}
	return 0;
}

链接：戳这里

  历届试题 城市建设  

时间限制：1.0s   内存限制：256.0MB

    

问题描述

　　栋栋居住在一个繁华的C市中，然而，这个城市的道路大都年久失修。市长准备重新修一些路以方便市民，于是找到了栋栋，希望栋栋能帮助他。

　　C市中有n个比较重要的地点，市长希望这些地点重点被考虑。现在可以修一些道路来连接其中的一些地点，每条道路可以连接其中的两个地点。另外由于C市有一条河从中穿过，也可以在其中的一些地点建设码头，所有建了码头的地点可以通过河道连接。

　　栋栋拿到了允许建设的道路的信息，包括每条可以建设的道路的花费，以及哪些地点可以建设码头和建设码头的花费。

　　市长希望栋栋给出一个方案，使得任意两个地点能只通过新修的路或者河道互达，同时花费尽量小。

输入格式

　　输入的第一行包含两个整数n, m，分别表示C市中重要地点的个数和可以建设的道路条数。所有地点从1到n依次编号。
　　接下来m行，每行三个整数a, b, c，表示可以建设一条从地点a到地点b的道路，花费为c。若c为正，表示建设是花钱的，如果c为负，则表示建设了道路后还可以赚钱（比如建设收费道路）。
　　接下来一行，包含n个整数w_1, w_2, …, w_n。如果w_i为正数，则表示在地点i建设码头的花费，如果w_i为-1，则表示地点i无法建设码头。
　　输入保证至少存在一个方法使得任意两个地点能只通过新修的路或者河道互达。

输出格式

　　输出一行，包含一个整数，表示使得所有地点通过新修道路或者码头连接的最小花费。如果满足条件的情况下还能赚钱，那么你应该输出一个负数。

样例输入

5 5
1 2 4
1 3 -1
2 3 3
2 4 5
4 5 10
-1 10 10 1 1

样例输出

9

样例说明

　　建设第2、3、4条道路，在地点4、5建设码头，总的花费为9。

数据规模和约定

　　对于20%的数据，1<=n<=10，1<=m<=20，0<=c<=20，w_i<=20；
　　对于50%的数据，1<=n<=100，1<=m<=1000，-50<=c<=50，w_i<=50；
　　对于70%的数据，1<=n<=1000；
　　对于100%的数据，1 <= n <= 10000，1 <= m <= 100000，-1000<=c<=1000，-1<=w_i<=1000，w_i≠0。

 

思路：

首先处理不需要建设码头的最小生成树  得到值ans。

然后 加一个0点 连接可以建设的每一个码头   加入邻接表  跑最小生成树  去min

代码：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
#define INF 1e20
using namespace std;
int n,m,tot;
struct edge{
	int u,v,w,next,f;
} e[500100];
bool cmp(edge a,edge b){
	return a.w<b.w;
}
int fa[10010],head[10010],a[10010];
int find(int x){
	if(x!=fa[x]){
		fa[x]=find(fa[x]);
	}
	return fa[x];
}
void init(){
	for(int i=0;i<=n;i++) fa[i]=i;
	for(int i=1;i<=n;i++) head[i]=-1;
	tot=0;
}
void add(int U,int V,int W,int f){
	e[tot].u=U;
	e[tot].v=V;
	e[tot].w=W;
	e[tot].next=head[U];
	e[tot].f=f;
	head[U]=tot++;
}
int main(){
	scanf("%d%d",&n,&m);
	init();
	long long ans=0,sum=0,anw=INF;
	for(int i=1;i<=m;i++) {
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		if(w<0){
			add(u,v,0,0);
			add(v,u,0,0);
			ans+=(long long)-w;
		} else {
			add(u,v,w,0);
			add(v,u,w,0);
		}
	}
	sort(e,e+tot,cmp);
	for(int i=0;i<tot;i++){
		int xx=find(e[i].u);
		int yy=find(e[i].v);
		if(xx!=yy){
			fa[xx]=yy;
			sum+=(long long)e[i].w;
		}
	}
	int flag=0;
	for(int i=2;i<=n;i++){
		if(find(1)!=find(i)){
			flag=1;
			break;
		}
	}
	if(!flag) anw=min(anw,sum);
	///printf("%I64d\n",anw);
	for(int i=1;i<=n;i++) {
		scanf("%d",&a[i]);
		if(a[i]!=-1) {
			add(0,i,a[i],1);
			add(i,0,a[i],1);
		}
	}
	sort(e,e+tot,cmp);
	for(int i=0;i<=n;i++) fa[i]=i;
	sum=0;
	for(int i=0;i<tot;i++){
		int xx=find(e[i].u);
		int yy=find(e[i].v);
		if(xx!=yy){
			fa[xx]=yy;
			sum+=(long long)e[i].w;
		}
	}
	///printf("%I64d %I64d\n",anw,sum);
	anw=min(anw,sum);
	printf("%I64d\n",anw-ans);
	return 0;

}
/*
5 5
1 3 10
1 2 10
2 3 10
2 4 10
4 5 10
1 1 1 1 1

5 10
5 2 8
4 5 8
2 5 10
1 4 4
5 3 5
1 2 9
1 5 8
5 1 2
1 3 5
4 3 12
-1 -1 -1 18 11 
19
*/