【C】分治算法
分治算法虽然听起来有可能有点陌生,但是实质上绝对是见过。比如在有序顺序表中的二分查找就是分治法的其中一个实例。它的时间复杂度经常性能把一个问题从O(n)降为O(nlogn),虽然它的代码往往涉及到递归调用,看起来非常复杂。
比如以下的一个简单得不能再简单的问题,求数组int a[4]={1,3,2,4}的最大值。第一反应想都不用想就得出如下的代码:
#include<stdio.h>
void main(){
int a[4]={1,3,2,4};
int max=a[0];
for(int i=0;i<4;i++){
if(max<a[i]){
max=a[i];
}
}
printf("%d",max);
}
先设定最大值为a[0],然后遍历这个数组的每一个元素,看它是否大于最大值,如果是,设这个元素为最大值,时间复杂度为O(n),这里4个元素,就要比较4次。
然而,如果用分治法去比较:
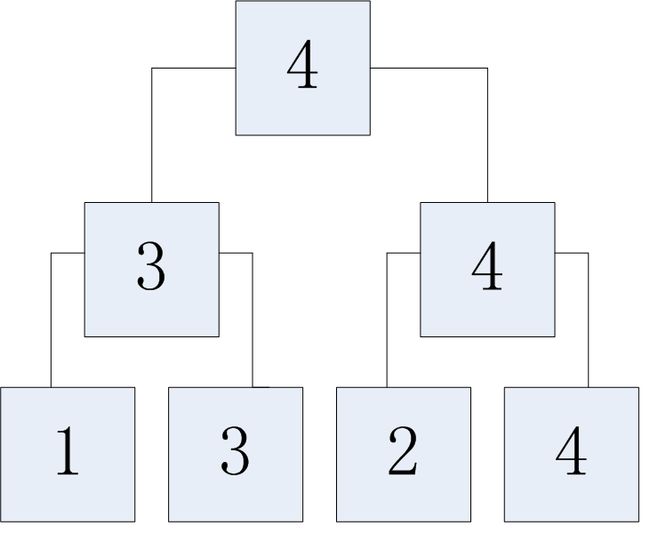
不停地将数组拆分成n/2,直到无法再分割,就比如这里4个元素{1,3,2,4},先将其拆分成{1,3},{2,4},已经无法再拆分了,就先从各个小元组中最大值再组成数组{3,4},从而再从这个新数组中,求最大值为4,这里仅比较3次,{1,3},{2,4}的时候2次,{3,4}1次,时间复杂度为O(nlogn),从O(n)将成O(nlogn)是个了不起的成就,然而写成代码却是涉及到递归调用,无比地蛋疼:
#include<stdio.h>
int getMax(int array[], int begin, int end){
int Max1 = 0;
int Max2 = 0;
if (begin == end) {//划分到最后,剩余1个数
return array[begin] = array[end];
}
else if(begin+1==end){//划分到最后,剩余2个数
return array[begin]> array[end]?array[begin]: array[end];//谁大返回谁。
}
else{//如果剩余的数多于2个,划分成两段,选出这两段的最大值
int mid=(begin+end)/2;
Max1=getMax(array,begin,mid);
Max2=getMax(array,mid+1,end);
return Max1>Max2?Max1:Max2;
}
};
void main(){
int a[4]={1,3,2,4};
printf("%d",getMax(a,0,3));
}
然而,其时间复杂度却减少了,这就是分治算法。
下面再用一道2014年上半年的软件设计师软考题来说明这个问题,题目是这样的:
采用归并排序对n个元素进行递增排序时,首先将n个元素的数组分成各含n/2个元素的两个子数组,然后用归并排序对两个子数组进行递归排序,最后合并两个已经排好序的子数组得到排序结果,用C语言现实上述递归排序,其中常量和变量规定如下:arr是待排序的数组,一个子数组的位置从p到q,另一个子数组的位置从q+1到r,begin与end是待排序数组的起止位置,left与right是临时存放待合并的两个子数组,n1与n2为两个子数组的长度,i,j,k为循环变量,mid为临时变量。
#include<stdio.h>
#include<stdlib.h>
#define MAX 65536
void merge(int arr[],int p, int q,int r){
int *left,*right;
int n1,n2,i,j,k;
//计算左右数组应有的长度
n1=q-p+1;
n2=r-q;
//开拓左由数组的空间
if((left=(int*)malloc((n1+1)*sizeof(int)))==NULL){
perror("malloc error");
exit(1);
}
if((right=(int*)malloc((n2+1)*sizeof(int)))==NULL){
perror("malloc error");
exit(1);
}
//讲待排序数组的平分成两个n/2长的数组,分别存进左右数组
for(i=0;i<n1;i++){
left[i]=arr[p+i];
}
left[i]=MAX;//封口
for(i=0;i<n2;i++){
right[i]=arr[(q+1)+i];//q+1是右数组的起始位置,而不是q,注意!
}
right[i]=MAX;//封口
i=0,j=0;
for(k=p;k<=r;k++){//选择左右数组的小者,放入排序后的数组,也就是覆盖原来的数组中存在的内容
if(left[i]>right[j]){
arr[k]=right[j];
j++;
}else{
arr[k]=left[i];
i++;
}
}
}
void mergeSort(int arr[],int begin,int end){
int mid;
if(begin<end){//如果begin=end或者begin>end,证明分无可分,就不分了
mid=(begin+end)/2;//将数组分成2半
mergeSort(arr,begin,mid);//要求对左部分进行排序
mergeSort(arr,mid+1,end);//要求对右部分进行排序
merge(arr,begin,mid,end);//真正的排序算法
}
}
void main(){
int a[4]={4,2,1,3};
mergeSort(a,0,3);
for(int i=0;i<4;i++){
printf("%d",a[i]);
}
}
这里的各趟递归,排序之后的结果如下所示:
归并排序的最好、最坏和平均时间复杂度都是O(nlogn),而空间复杂度是O(n),比较次数介于(nlogn)/2和(nlogn)-n+1,赋值操作的次数是(2nlogn)。因此可以看出,归并排序算法比较占用内存,但却是效率高且稳定的排序算法。这里涉及到对递归式f(n)=2*f(n/2)+O(n)的分析,比较难,记住它就行。
比起最简单的冒泡排序O(n2),时间复杂度降低得非常明显。