hdoj 3820 Golden Eggs 【双二分图构造最小割模型】
Golden EggsTime Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 505 Accepted Submission(s): 284
Problem Description
There is a grid with N rows and M columns. In each cell you can choose to put a golden or silver egg in it, or just leave it empty. If you put an egg in the cell, you will get some points which depends on the color of the egg. But for every pair of adjacent eggs with the same color, you lose G points if there are golden and lose S points otherwise. Two eggs are adjacent if and only if there are in the two cells which share an edge. Try to make your points as high as possible.
Input
The first line contains an integer T indicating the number of test cases.
There are four integers N, M, G and S in the first line of each test case. Then 2*N lines follows, each line contains M integers. The j-th integer of the i-th line Aij indicates the points you will get if there is a golden egg in the cell(i,j). The j-th integer of the (i+N)-th line Bij indicates the points you will get if there is a silver egg in the cell(i,j). Technical Specification 1. 1 <= T <= 20 2. 1 <= N,M <= 50 3. 1 <= G,S <= 10000 4. 1 <= Aij,Bij <= 10000
Output
For each test case, output the case number first and then output the highest points in a line.
Sample Input
Sample Output
|
自己AC的,没有看任何题解。1A后好激动!
强烈建议做过 方格填数(2) 和 Game 之后,再做这道题!!!
理解好的话,解决这道题应该没什么问题。
题意:
有一个N*M个格子,你可以选择向每一个格子放一个金蛋或一个银蛋或什么都不放。
给你两个N*M矩阵
第一个N*M矩阵表示在i行第j列的格子放置一个金蛋能获得的价值,第二个N*M矩阵表示第i行第j列的格子放置一个银蛋能获得的价值。
又给出两个限制
1,若相邻的格子放的全是金蛋,则你的价值总和要减去G。
2,若相邻的格子放的全是银蛋,则你的价值总和要减去S。
问你能够得到的最大价值。
思路:构造两个二分图。
第一个二分图表示金蛋,以横纵坐标和为奇数的点集为S1集,横纵坐标和为偶数的点集为T1集。
第二个二分图表示银蛋,以横纵坐标和为奇数的点集为S2集,横纵坐标和为偶数的点集为T2集。
我们知道
1, 一个格子 x 不能既放金蛋又放银蛋,则有S1集 -> S2集建边无穷大,意味着同时选中S1和S2集 里的格子x需要付出的代价为无穷大——不能去掉这条边,对T1集和T2集也是如此建边。
2,相邻格子不能选择相同蛋,则S集->T集建边,容量为选择相同蛋需要付出的代价。
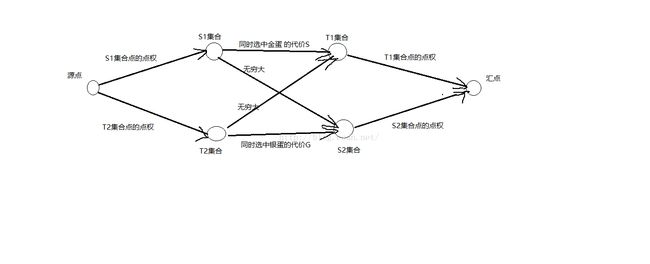
给个图示
建图思路:设置超级源点source,超级汇点sink。
1,source向S1集和T2集的点建边,容量为点权;
2,T1集和S2集的点向sink建边,容量为点权;
3,S1集向T1集建边,容量为相邻格子同时选中金蛋付出的代价G;
4,T2集向S2集建边,容量为相邻格子同时选中银蛋付出的代价S;
5,S1集向S2集建边,容量为无穷大,表示同一个格子不能同时放金蛋和银蛋;
6,T2集向T1集建边,容量为无穷大,表示同一个格子不能同时放金蛋和银蛋。
最后求出最大流——最小割,用金蛋银蛋总价值减去最小割就行了。
AC代码:
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#define MAXN 6000
#define MAXM 50000
#define INF 0x3f3f3f3f
using namespace std;
struct Edge
{
int from, to, cap, flow, next;
};
Edge edge[MAXM];
int head[MAXN], edgenum;
int dist[MAXN], cur[MAXN];
bool vis[MAXN];
int N, M, G, S;
void init()
{
edgenum = 0;
memset(head, -1, sizeof(head));
}
void addEdge(int u, int v, int w)
{
Edge E1 = {u, v, w, 0, head[u]};
edge[edgenum] = E1;
head[u] = edgenum++;
Edge E2 = {v, u, 0, 0, head[v]};
edge[edgenum] = E2;
head[v] = edgenum++;
}
int point(int x, int y)
{
return (x-1) * M + y;
}
bool judge(int x, int y)
{
return x >= 1 && x <= N && y >= 1 && y <= M;
}
int sum;//金蛋 银蛋的总价值
int source, sink;
void getMap()
{
source = 0, sink = N * M * 2 + 1;
sum = 0;
int a;
for(int i = 1; i <= N; i++)
{
for(int j = 1; j <= M; j++)
{
scanf("%d", &a);
sum += a;
if((i+j) & 1)//源点 连 S1集
addEdge(source, point(i, j), a);
else//T1集 连汇点
addEdge(point(i, j), sink, a);
}
}
for(int i = 1; i <= N; i++)
{
for(int j = 1; j <= M; j++)
{
scanf("%d", &a);
sum += a;
if((i+j) & 1)//S2集 连汇点
addEdge(point(i, j) + N*M, sink, a);//S2集合 x 格子的编号为S1集合 x 格子编号 + N*M
else//源点连 T2集
addEdge(source, point(i, j) + N*M, a);
}
}
int move[4][2] = {0,1, 0,-1, 1,0, -1,0};
for(int i = 1; i <= N; i++)
{
for(int j = 1; j <= M; j++)
{
for(int k = 0; k < 4; k++)
{
int x = i + move[k][0];
int y = j + move[k][1];
if(!judge(x, y)) continue;
if((i+j) & 1)//S1集
{
addEdge(point(i, j), point(i, j) + N*M, INF);//S1集 向 S2集建边无穷大 表示不能同时选
if((x+y) % 2 == 0)
addEdge(point(i, j), point(x, y), G);//S1集 向 T1集建边
}
else//T1集
{
addEdge(point(i, j) + N*M, point(i, j), INF);//T2集 向 T1集建边无穷大 表示不能同时选
if((x+y) & 1)
addEdge(point(i, j)+N*M, point(x, y) + N*M, S);//T2集 向 S2集建边
}
}
}
}
}
bool BFS(int s, int t)
{
queue<int> Q;
memset(dist, -1, sizeof(dist));
memset(vis, false, sizeof(vis));
dist[s] = 0;
vis[s] = true;
Q.push(s);
while(!Q.empty())
{
int u = Q.front();
Q.pop();
for(int i = head[u]; i != -1; i = edge[i].next)
{
Edge E = edge[i];
if(!vis[E.to] && E.cap > E.flow)
{
dist[E.to] = dist[u] + 1;
if(E.to == t) return true;
vis[E.to] = true;
Q.push(E.to);
}
}
}
return false;
}
int DFS(int x, int a, int t)
{
if(x == t || a == 0) return a;
int flow = 0, f;
for(int &i = cur[x]; i != -1; i = edge[i].next)
{
Edge &E = edge[i];
if(dist[E.to] == dist[x] + 1 && (f = DFS(E.to, min(a, E.cap-E.flow), t)) > 0)
{
edge[i].flow += f;
edge[i^1].flow -= f;
flow += f;
a -= f;
if(a == 0) break;
}
}
return flow;
}
int Maxflow(int s, int t)
{
int flow = 0;
while(BFS(s, t))
{
memcpy(cur, head, sizeof(head));
flow += DFS(s, INF, t);
}
return flow;
}
int main()
{
int t, k = 1;
scanf("%d", &t);
while(t--)
{
scanf("%d%d%d%d", &N, &M, &G, &S);
init();
getMap();
printf("Case %d: %d\n", k++, sum - Maxflow(source, sink));
}
return 0;
}