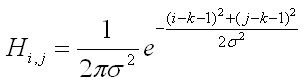数字图像处理03（卷积、滤波、边缘检测——算法原理）
1.首先介绍一下相关和卷积的关系：
图像滤波的计算过程分析
滤波通常是用卷积或者相关来描述，而线性滤波一般是通过卷积来描述的。他们非常类似，但是还是会有不同。下面我们来根据相关和卷积计算过程来体会一下他们的具体区别：
卷积的计算步骤：
（1）卷积核绕自己的核心元素顺时针旋转180度
（2）移动卷积核的中心元素，使它位于输入图像待处理像素的正上方
（3）在旋转后的卷积核中，将输入图像的像素值作为权重相乘
（4）第三步各结果的和做为该输入像素对应的输出像素
相关的计算步骤：
（1）移动相关核的中心元素，使它位于输入图像待处理像素的正上方
（2）将输入图像的像素值作为权重，乘以相关核
（3）将上面各步得到的结果相加做为输出
可以看出他们的主要区别在于计算卷积的时候，卷积核要先做旋转。而计算相关过程中不需要旋转相关核。
在matlab中，这个比较有区分，然而在opencv中，所讨论的卷积滤波都是对应像素求权重和，并没有发现将核旋转（故我个人人为是相关操作）
2.高斯函数、高斯卷积
高斯函数：
可以发现很多教材以及网上的资料都描述高斯滤波的原理是采用高斯算子对图像进行卷积运算。其实在各个算法库如Matlab、OpenCV等，在实现的时候，就是采用一个矩阵模板进行加权运算，拿图像的八连通区域来说，中间点的像素值就等于八连通区的像素值的均值，这样达到平滑的效果，该模板我们常成为高斯核。
根据上述分析可知，高斯核是整个求解的关键。很显然，它是通过二维高斯函数计算得来的。这里给出离散高斯核矩阵的计算公式。
离散的高斯卷积核H： (2k+1)×(2k+1)维，其元素计算方法为：
其中Sigma为方差，k确定核矩阵的维数，关于这两个取值，在下文进行分析。
与matlab函数运行结果对比
这里对高斯卷积核的矩阵算法进行验证。
1）在matlab中用以下代码可以产生一个3×3的核。
filter=fspecial('gaussian',3,1);
所产生的核矩阵为：
filter =
0.0751 0.1238 0.0751
0.1238 0.2042 0.1238
0.0751 0.1238 0.0751
&n`sp;2）同样对于上述的公式，我们取k=1，Sigma=1，即可得到3×3的高斯卷积核如下：
上文说到，我们进行加权滤波，权系数之和必须为1，上面所求出的高斯滤波核函数同样的必须进行归一化：
由此可以证明该核函数计算方法的正确性。
3.laplace算子
很简单：x方向和y方向分别求导数（二阶导数），然后将两个方向的导数直接求和，就得到这个值。当然，数字图像求导数就是求差分，也即核和原图卷积。laplace公式如下：
4.梯度算子(一阶导数)
一阶导数梯度定义如下：
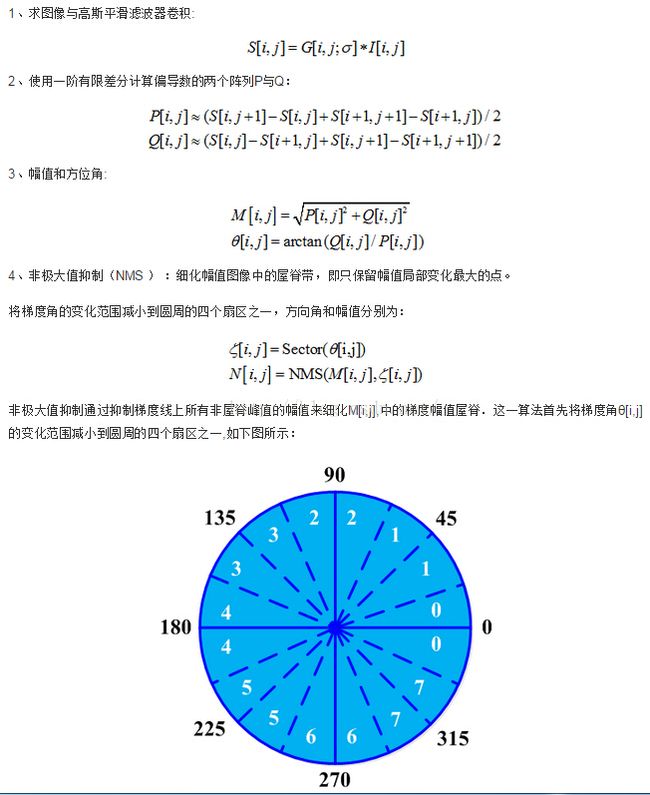
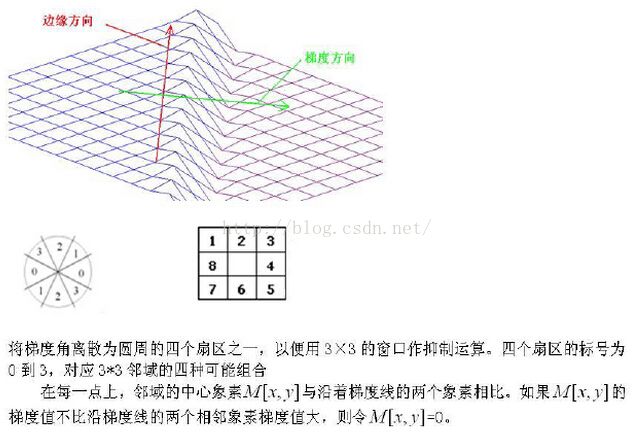
5.canny算子
取阈值
-
将低于阈值的所有值赋零，得到图像的边缘阵列
- 阈值τ取得太低->假边缘
- 阈值τ取得太高->部分轮廊丢失
- 选用两个阈值: 更有效的阈值方案．
- 链接
