LeetCode Maximal Rectangle

Maximal Rectangle

Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing all ones and return its area.

一道超难的题目，思想难，同时实现也难。

本题是动态规划法的高级应用，还依据题目特征优化，难度相当高。

经提示，知道是max histogram这个题目的思想的灵活运用，就是每一行运用max histogram算法思想计算。

原来LeetCode把max histogram放在这一题之前是有原因的。没有max histogram这一题的思想基础垫底，是很难理解的。

LeetCode论坛上的讨论，其实也是这一思想的变种运用，不过感觉讲得并不清楚，他所谓的拖线法，其实就是histogram的倒置。

只不过并没有严格按照histogram的算法来进行，而是优化了。

我按histogram算法写的程序用了大概100ms左右，他的算法程序能在40-50ms左右，很快。

所以我也不得不研究一下他的算法到底优化了什么。

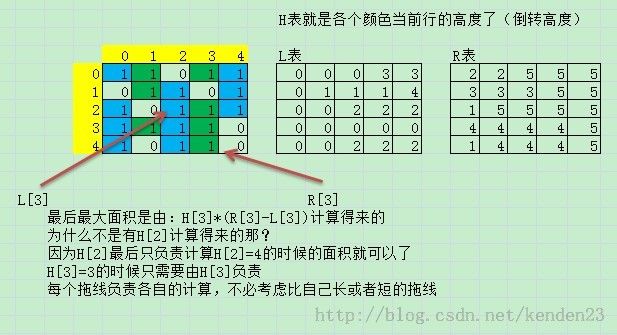
他使用了三个表L，R，H表，我也画了三个表，对比看看，填填这个表，就能理解这个算法了：

下面是标准的histogram题目算法的应用程序：

 class Solution {
 public:
     int maximalRectangle(vector<vector<char> > &matrix)
     {
         int row = matrix.size();
         if (row < 1) return 0;
         int col = matrix[0].size();
         vector<int> his(col);
         int maxArea = 0;

         for (int i = row-1; i >= 0; i--)
         {
             formHistogram(matrix, i, his);
             maxArea = max(maxArea, maxHistogram(his));
         }
         return maxArea;
     }

     void formHistogram(vector<vector<char> > &m, int row, vector<int> &his)
     {
         for (size_t j = 0; j < m[0].size(); j++)
         {
             if (m[row][j]-'0' == 0) his[j] = 0;
             else if (row != m.size()-1 && m[row+1][j]-'0' == 1)
             {
                 his[j]--;
             }
             else
             {
                 for (int i = row; i >= 0; i--)
                 {
                     if (m[i][j]-'0' == 1) his[j]++;
                     else break;
                 }
             }
         }
     }
     int maxHistogram(vector<int> &h)
     {
         h.push_back(0);
         int n = h.size();
         int maxArea = 0;
         stack<int> stk;

         for (int i = 0; i < n; )
         {
             if (stk.empty() || h[stk.top()] <= h[i]) stk.push(i++);
             else
             {
                 int t = stk.top();
                 stk.pop();
                 maxArea = max(maxArea, h[t]*(stk.empty()? i:i-stk.top()-1));
             }
         }
         return maxArea;
     }
 };

优化一点histogram算法的程序：

 int maxHistogram(vector<int> &h)
     {
         h.push_back(0);
         int n = h.size();
         int maxArea = 0;
         stack<int> stk;

         for (int i = 0; i < n; )
         {
             if (stk.empty() || h[stk.top()] <= h[i]) stk.push(i++);
             else
             {
                 int t = stk.top();
                 stk.pop();
                 maxArea = max(maxArea, h[t]*(stk.empty()? i:i-stk.top()-1));
             }
         }
         return maxArea;
     }
     //================histogram，拖线法实现
     int maximalRectangle2(vector<vector<char> > &matrix)
     {
         int row = matrix.size();
         if (row < 1) return 0;
         int col = matrix[0].size();
         vector<int> his(col);
         int maxArea = 0;

         for (int i = row-1; i >= 0; i--)
         {
             for (int j = 0; j < col; j++)
             {
                 if ( matrix[i][j]-'0' == 1) his[j]++;
                 else his[j] = 0;
             }

             maxArea = max(maxArea, maxHistogram(his));
         }
         return maxArea;
     }

最后是leetcode上的优化算法，也是上图示意图的算法实现：

 int maximalRectangle(vector<vector<char> > &matrix) {
         if (matrix.empty()) {
             return 0;
         }

         int n = matrix[0].size();
         vector<int> H(n);
         vector<int> L(n);
         vector<int> R(n, n);

         int ret = 0;
         for (int i = 0; i < matrix.size(); ++i) {
             int left = 0, right = n;
             // calculate L(i, j) from left to right
             for (int j = 0; j < n; ++j) {
                 if (matrix[i][j] == '1') {
                     ++H[j];
                     L[j] = max(L[j], left);
                 }
                 else {
                     left = j+1;
                     H[j] = 0; L[j] = 0; R[j] = n;
                 }
             }
             // calculate R(i, j) from right to right
             for (int j = n-1; j >= 0; --j) {
                 if (matrix[i][j] == '1') {
                     R[j] = min(R[j], right);
                     ret = max(ret, H[j]*(R[j]-L[j]));
                 }
                 else {
                     right = j;
                 }
             }
         }

         return ret;
     }

2014-2-27 update：

还是下面这个程序比较保险，虽然leetcode上测试，是上一个程序比较快，但是按照理论上计算，两个算法的时间复杂度都是O(n*n)，而空间复杂度也都是O(n)，那么其实两个方法的实际运行速度都应该差不多的。

而且主要是下面这个程序更加模块化，更简易；上一个程序很容易出错，下标处理起来很麻烦的，一不小心结果就会出错。

 int maximalRectangle(vector<vector<char> > &matrix)
     {
         if (matrix.empty() || matrix[0].empty()) return 0;
         vector<int> height(matrix[0].size()+1);
         int max_area = 0;
         for (int i = 0; i < matrix.size(); i++)
         {
             for (int j = 0; j < matrix[0].size(); j++)
             {
                 if (matrix[i][j] == '1') height[j]++;
                 else height[j] = 0;
             }
             max_area = max(max_area, maxHistogram(height));
         }
         return max_area;
     }
     int maxHistogram(vector<int> &height)
     {
         int ans = 0;
         stack<int> stk;
         for (int i = 0; i < height.size(); )
         {
             if (stk.empty() || height[stk.top()] < height[i]) stk.push(i++);
             else
             {
                 int idx = stk.top();
                 stk.pop();
                 ans = max(ans, (stk.empty()? i:i-stk.top()-1)*height[idx]);
             }
         }
         return ans;
     }