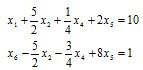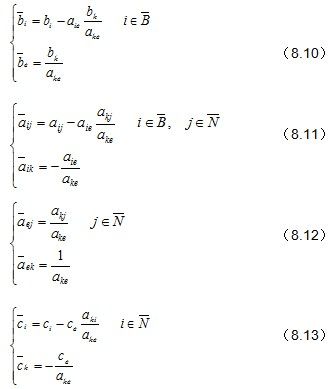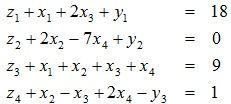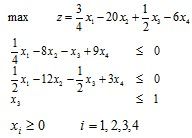【线性规划】单纯形算法(未完全实现)

 题外话：王晓东的《算法设计与分析》看到现在，终于遇到自己琢磨不透的代码了。这里粘出来，求大神指点迷津，将代码补充完整~

    1、线性规划问题及其表示

    线性规划问题可表示为如下形式：

    变量满足约束条件(8.2)-(8.5)式的一组值称为线性规划问题的一个可行解。
    所有可行解构成的集合称为线性规划问题的可行区域。
    使目标函数取得极值的可行解称为最优解。
    在最优解处目标函数的值称为最优值。
    有些情况下可能不存在最优解。
    通常有两种情况：
    (1)根本没有可行解，即给定的约束条件之间是相互排斥的，可行区域为空集；
    (2)目标函数没有极值，也就是说在n 维空间中的某个方向上，目标函数值可以无限增大，而仍满足约束条件，此时目标函数值无界。

    例：

     

     这个问题的解为 (x1,x2,x3,x4) = (0,3.5,4.5,1)；最优值为16。 

    2、线性规划基本定理

     约束条件(8.2)-(8.5)中n个约束以等号满足的可行解称为线性规划问题的基本可行解。
    若n>m，则基本可行解中至少有n-m个分量为0，也就是说，基本可行解中最多有m个分量非零。
    线性规划基本定理：如果线性规划问题有最优解，则必有一基本可行最优解。
    上述定理的重要意义在于，它把一个最优化问题转化为一个组合问题，即在(8.2) -(8.5)式的m+n个约束条件中，确定最优解应满足其中哪n个约束条件的问题。
    由此可知，只要对各种不同的组合进行测试，并比较每种情况下的目标函数值，直到找到最优解。
    Dantzig于1948年提出了线性规划问题的单纯形算法。
    单纯形算法的特点是：
  （1）只对约束条件的若干组合进行测试，测试的每一步都使目标函数的值增加；
  （2）一般经过不大于m或n次迭代就可求得最优解。     

    3、约束标准型线性规划问题的单纯形算法 

    当线性规划问题中没有不等式约束(8.2)和(8.4)式，而只有等式约束(8.3)和变量非负约束(8.5)时，称该线性规划问题具有标准形式。
    先考察一类更特殊的标准形式线性规划问题。这一类线性规划问题中，每一个等式约束中，至少有一个变量的系数为正，且这个变量只在该约束中出现。
    在每一约束方程中选择一个这样的变量，并以它作为变量求解该约束方程。这样选出来的变量称为左端变量或基本变量，其总数为m个。剩下的n-m个变量称为右端变量或非基本变量。
    这一类特殊的标准形式线性规划问题称为约束标准型线性规划问题。
    虽然约束标准型线性规划问题非常特殊，但是对于理解线性规划问题的单纯形算法是非常重要的。
    任意一个线性规划问题可以转换为约束标准型线性规划问题。

     例：

      

      

     任何约束标准型线性规划问题，只要将所有非基本变量都置为0，从约束方程式中解出满足约束的基本变量的值，可求得一个基本可行解。
     单纯形算法的基本思想就是从一个基本可行解出发，进行一系列的基本可行解的变换。
     每次变换将一个非基本变量与一个基本变量互调位置，且保持当前的线性规划问题是一个与原问题完全等价的标准线性规划问题。
     基本可行解x=(7,0,0,12,0,10)。
     单纯形算法的第1步：选出使目标函数增加的非基本变量作为入基变量。
    查看单纯形表的第1行（也称之为z行）中标有非基本变量的各列中的值。
    选出使目标函数增加的非基本变量作为入基变量。
    z行中的正系数非基本变量都满足要求。
    在上面单纯形表的z行中只有1列为正，即非基本变量相应的列，其值为3。
    选取非基本变量x3作为入基变量。
    单纯形算法的第2步：选取离基变量。
    在单纯形表中考察由第1步选出的入基变量所相应的列。
    在一个基本变量变为负值之前，入基变量可以增到多大。

    如果入基变量所在的列与基本变量所在行交叉处的表元素为负数，那么该元素将不受任何限制，相应的基本变量只会越变越大。
    如果入基变量所在列的所有元素都是负值，则目标函数无界，已经得到了问题的无界解。
    如果选出的列中有一个或多个元素为正数，要弄清是哪个数限制了入基变量值的增加。
    受限的增加量可以用入基变量所在列的元素（称为主元素）来除主元素所在行的“常数列”（最左边的列）中元素而得到。所得到数值越小说明受到限制越多。
    应该选取受到限制最多的基本变量作为离基变量，才能保证将入基变量与离基变量互调位置后，仍满足约束条件。
    上例中，惟一的一个值为正的z行元素是3，它所在列中有2个正元素，即4和3。
    min{12/4,10/3}=4，应该选取x4为离基变量；
    入基变量x3取值为3。
    单纯形算法的第3步：转轴变换。
    转轴变换的目的是将入基变量与离基变量互调位置。
    给入基变量一个增值，使之成为基本变量；
    修改离基变量，让入基变量所在列中，离基变量所在行的元素值减为零，而使之成为非基本变量。

    解离基变量所相应的方程，将入基变量x3用离基变量x4表示为

    再将其代入其他基本变量和所在的行中消去x3 ，

     

    代入目标函数得到

    形成新单纯形表

     

     单纯形算法的第4步：转回并重复第1步，进一步改进目标函数值。
     不断重复上述过程，直到z行的所有非基本变量系数都变成负值为止。这表明目标函数不可能再增加了。
     在上面的单纯形表中，惟一的值为正的z行元素是非基本变量x2相应的列，其值为1/2。
     因此，选取非基本变量x2作为入基变量。
     它所在列中有惟一的正元素5/2，即基本变量x1相应行的元素。
     因此，选取x1为离基变量。
     再经步骤3的转轴变换得到新单纯形表。

     新单纯形表z行的所有非基本变量系数都变成负值，求解过程结束。

    整个问题的解可以从最后一张单纯形表的常数列中读出。
    目标函数的最大值为11；
    最优解为：x*=(0,4,5,0,0,11)。

    

     单纯形算法计算步骤如下：
    步骤1：选入基变量。
    如果所有cj0，则当前基本可行解为最优解，计算结束。
    否则取ce>0相应的非基本变量xe为入基变量。
    步骤2：选离基变量。
    对于步骤1选出的入基变量xe ，如果所有aie0 ，则最优解无界，计算结束。
    否则计算

     

    选取基本变量xk为离基变量。
    新的基本变量下标集为
    新的非基本变量下标集为
    步骤3：作转轴变换。
    新单纯形表中各元素变换如下。

     

    步骤4：转步骤1。

    4、将一般问题转化为约束标准型    

    有几种巧妙的办法可以将一般的线性规划问题转换为约束标准型线性规划问题。
    首先，需要把(8.2)或(8.4)形式的不等式约束转换为等式约束。
    具体做法是，引入松弛变量，利用松弛变量的非负性，将不等式转化为等式。
    松驰变量记为yi，共有m1+m3个。
    在求解过程中，应当将松弛变量与原来变量同样对待。求解结束后，抛弃松弛变量。
    注意松弛变量前的符号由相应的原不等式的方向所确定。

    

    为了进一步构造标准型约束，还需要引入m个人工变量，记为zi。
    至此，原问题已经变换为等价的约束标准型线性规划问题。
    对极小化线性规划问题，只要将目标函数乘以-1即可化为等价的极大化线性规划问题。

     

     5、一般线性规划问题的2阶段单纯形算法 

     引入人工变量后的线性规划问题与原问题并不等价，除非所有zi都是0 。
    为了解决这个问题，在求解时必须分2个阶段进行。
    第一阶段用一个辅助目标函数替代原来的目标函数。
    这个线性规划问题称为原线性规划问题所相应的辅助线性规划问题。
    对辅助线性规划问题用单纯形算法求解。
    如果原线性规划问题有可行解，则辅助线性规划问题就有最优解，且其最优值为0，即所有zi都为0。
    在辅助线性规划问题最后的单纯形表中，所有zi均为非基本变量。
    划掉所有zi相应的列，剩下的就是只含xi和yi的约束标准型线性规划问题了。
    单纯形算法第一阶段的任务就是构造一个初始基本可行解。
    单纯形算法第二阶段的目标是求解由第一阶段导出的问题。
    此时要用原来的目标函数进行求解。
    如果在辅助线性规划问题最后的单纯形表中， zi不全为0，则原线性规划问题没有可行解，从而原线性规划问题无解。

     6、一般线性规划问题的2阶段单纯形算法 

     用单纯形算法解一般的线性规划问题时，可能会遇到退化的情形，即在迭代计算的某一步中，常数列中的某个元素的值变成0，使得相应的基本变量取值为0。
     如果选取退化的基本变量为离基变量，则作转轴变换前后的目标函数值不变。在这种情况下，算法不能保证目标函数值严格递增，因此，可能出现无限循环。
     考察下面的由Beale在1955年提出的退化问题的例子。
     按照2阶段单纯形算法求解该问题将出现无限循环。

     

     Bland提出避免循环的一个简单易行的方法。
     Bland提出在单纯形算法迭代中，按照下面的2个简单规则就可以避免循环。

     规则1：设，取xe为入基变量。
     规则2：设 

     取xk为离基变量。
     算法leave(col)已经按照规则2选取离基变量。
     选取入基变量的算法enter(objrow) 中只要加一个break语句即可。

     7、算法描述和实现

 //线性规划 单纯性算法
 #include "stdafx.h"
 #include <cmath>
 #include <iostream>
 #include<fstream>
 using namespace std;

 class LinearProgram
 {
     public:
         LinearProgram(char * filename);
         ~LinearProgram();
         void solve();
     private:
         int enter(int objrow);
         int leave(int col);
         int simplex(int objrow);
         int phase1();
         int phase2();
         int compute();
         void swapbasic(int row,int col);
         void pivot(int row,int col);
         void stats();//这个方法是干什么的？
         void setbasic(int * basicp);
         void output();
         int m,              //约束总数
             n，              //变量数
             m1,             //不等式约束数<=
             m2,             //等式约束
             m3,             //不等式约束数>=
             n1,n2,          //n1 = n + m3,n2 = n1 + m1
             error,          //记录错误类型
             *basic,         //基本变量下标
             *nonbasic;      //非基本变量下标
         double **a,minmax;
 };

 //从标准输入文件中读入数据，构造初始单纯形表
 LinearProgram::LinearProgram(char *filename)
 {
     ifstream inFile;
     int i,j;
     double value;
     cout<<"按照下列格式输入数据："<<endl;
     cout<<"1:+1(max)或-1(min);m;n"<<endl;
     cout<<"2:m1;m2;m3"<<endl;
     cout<<"约束系数和右端项"<<endl;
     cout<<"目标函数系数"<<endl;
     error = 0;

     inFile.open(filename);
     inFile>>minmax;
     inFile>>m;
     inFile>>n;

     //输入各类约束数
     inFile>>m1;
     inFile>>m2;
     inFile>>m3;

     if(m!=m1+m2+m3)
     {
         error = 1;
     }

     n1 = n + m3;
     n2 = n + m1 + m3;
     Make2DArray(a,m+2,n1+1);//构造二维数组
     basic = new int[m+2];
     nonbasic = new int[n1+1];

     //初始化基本变量和非基本变量
     for(int i=0; i<=m+1; i++)
     {
         for(int j=0; j<=n1; j++)
         {
             a[i][j] = 0;
         }
     }

     for(int j=0; j<=n1; j++)
     {
         nonbasic[j] = j;
     }

     //引入松弛变量和人工变量
     for(int i=1,j=n1+1; i<=m; i++,j++)
     {
         basic[i] = j;
     }
     for(int i=m-m3+1,j=n+1; i<=m; i++,j++)
     {
         a[i][j] = -1.0;
         a[m+1][j] = -1.0;
     }

     //输入约束系数和右端项
     for(int i=1; i<=m; i++)
     {
         for(int j=1; j<=n; j++)
         {
             inFile>>value;
             a[i][j] = value;
         }
         inFile>>value;
         if(value<0)
         {
             error = 1;
         }
         a[i][0] = value;
     }

     //输入目标函数系数
     for(int j=1; j<=n; j++)
     {
         inFile>>value;
         a[0][j] = value * minmax;
     }

     //引入人工变量，构造第1阶段的辅助目标函数
     for(int j=1; j<=n;  j++)
     {
         for(int i=m1+1,value=0.0; i<=m; i++)
         {
             value += a[i][j];
         }
         a[m+1][j] = value;
     }
     inFile.close();
 }

 //根据目标函数系数所在的行objrow，执行约束标准型线性规划问题的单纯形算法
 int LinearProgram::simplex(int objrow)
 {
     for(int row = 0;;)
     {
         int col = enter(objrow);
         if(col>0)
         {
             row = leave(col);
         }
         else
         {
             return 0;
         }
         if(row>0)
         {
             pivot(row,col);
         }
         else
         {
             return 2;
         }
     }
 }

 //根据目标函数系数所在行objrow，选取入基变量
 int LinearProgram::enter(int objrow)
 {
     double temp = DBL_EPSILON;  //?什么含义？
     for(int j=1,col=0; j<n1; j++)
     {
         if(nonbasic[j]<=n2 && a[objrow][j]>temp)
         {
             col = j;
             temp = a[objrow][j];
             break;          //Bland避免循环法则
         }
     }
     return col;
 }

 //根据入基变量所在列col,选取离基变量
 int LinearProgram::leave(int col)
 {
     double temp = DBL_MAX;      //怎么定义的？值为多少？
     for(int i=1,row=0; i<=m; i++)
     {
         double val = a[i][col];
         if(value>DBL_EPSLION)
         {
             val = a[i][0]/val;
             if(val<temp)
             {
                 row = i;
                 temp = val;
             }
         }
     }
     return row;
 }

 //以入基变量所在列col和离基变量所在行row交叉处元素a[row][col]为轴心，做转轴变换
 void LinearProgram::pivot(int row,int col)
 {
     for(int j=0; j<=n1; j++)
     {
         if(j!=col)
         {
             a[row][j] = a[row][j]/a[row][col];
         }
     }
     a[row][col] = 1.0/a[row][col];
     for(int i=0; i<m+1; i++)
     {
         if(i!=row)
         {
             for(int j=0; j<=n1; j++)
             {
                 if(j!=col)
                 {
                     a[i][j] = a[i][j] - a[i][col]*a[row][j];
                     if(fabs(a[i][j]<DBL_EPSLION)
                     {
                         a[i][j] = 0.0;
                     }
                 }
             }
         }
     }
     swapbasic(row,col);
 }

 //交换基本变量row和非基本变量col的位置
 void LinearProgram::swapbasic(int row,int col)
 {
     int temp = basic[row];
     basic[row] = nonbasic[col];
     nonbasic[col] = temp;
 }

 //对一般的线性规划问题执行两阶段单纯形算法
 int LinearProgram::compute()
 {
     if(error>0)
     {
         return error;
     }
     if(m!=m1)
     {
         error = phase1();
         if(error>0)
         {
             return error;
         }
     }
     rturn phase2();
 }

 //构造初始基本可行解的第一阶段单纯形算法由phase1()实现
 //辅助目标函数存储在数组a的第trows行
 int LinearProgram::phase1()
 {
     error = simplex(m+1);
     if(error>0)
     {
         return error;
     }
     for(int i=1; i<=m; i++)
     {
         if(basic[i]>n2)
         {
             if(a[i][0]>DBL_EPSILON)
             {
                 return 3;
             }
             for(int j=1; j<=n1; j++)
             {
                 if(fabs(a[i][j]>=DBL_EPSILON)
                 {
                     pivot(i,j);
                     break;
                 }
             }
         }
     }
     return 0;
 }

 //第二阶段根据第一阶段找到的基本可行解，对原来的目标函数用单纯形算法求解
 //原目标函数存储在数组a的第0行
 int LinearProgram::phase2()
 {
     return simplex(0);
 }

 //执行两阶段单纯形算法
 void LinearProgram::solve()
 {
     cout<<endl<<"* * * 线性规划---单纯形算法 * * *"<<endl<<endl;
     error = compute();
     switch(error)
     {
         case 0:output();break;
         case 1:cout<<"输入数据错误--"<<endl;break;
         case 2:cout<<"无界解--"<<endl;break;
         case 3:cout<<"无可行解--"<<endl;
     }
     cout<<"计算结束"<<endl;
 }

 //输出结果
 void LinearProgram::output()
 {
     int width = 8,*basicp;
     doube zero = 0.0;
     basicp = new int[n+m+1];
     setbasic(basicp);
     cout.setf(ios::fixed|ios::showpoint|ios::right);
     cout.precision(4);s
     stats();//?????这句话是执行什么了？
     cout<<endl<<"最优值："<<-minmax*a[0][0]<<endl<<endl;
     cout<<"最优解："<<endl<<endl;
     for(int j=1; j<=n; j++)
     {
         cout<<"x"<<j<<" =";
         if(basicp[j]!=0)
         {
             cout<<setw(width)<<a[basicp[j]][0];
         }
         else
         {
             cout<<setw(width)<<zero;
         }
         cout<<endl;
     }
     cout<<endl;
     delete []basicp;
 }

 int main()
 {
     return 0;
 }