HDOJ 4349 —— 卢卡斯定理
Xiao Ming's Hope
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1154 Accepted Submission(s): 793
Problem Description
Xiao Ming likes counting numbers very much, especially he is fond of counting odd numbers. Maybe he thinks it is the best way to show he is alone without a girl friend. The day 2011.11.11 comes. Seeing classmates walking with their girl friends, he coundn't help running into his classroom, and then opened his maths book preparing to count odd numbers. He looked at his book, then he found a question "C
(n,0)+C
(n,1)+C
(n,2)+...+C
(n,n)=?". Of course, Xiao Ming knew the answer, but he didn't care about that , What he wanted to know was that how many odd numbers there were? Then he began to count odd numbers. When n is equal to 1, C
(1,0)=C
(1,1)=1, there are 2 odd numbers. When n is equal to 2, C
(2,0)=C
(2,2)=1, there are 2 odd numbers...... Suddenly, he found a girl was watching him counting odd numbers. In order to show his gifts on maths, he wrote several big numbers what n would be equal to, but he found it was impossible to finished his tasks, then he sent a piece of information to you, and wanted you a excellent programmer to help him, he really didn't want to let her down. Can you help him?
Input
Each line contains a integer n(1<=n<=10
8)
Output
A single line with the number of odd numbers of C
(n,0),C
(n,1),C
(n,2)...C
(n,n).
Sample Input
1 2 11
Sample Output
2 2 8
Author
HIT
Source
2012 Multi-University Training Contest 5
Recommend
zhuyuanchen520
题意是给你一个n,输出C(n,1),C(n,2)。。。C(n,n)中奇数的个数。
有一个结论是C(n , k)为奇数当且仅当(n&k) == k 。
然后根据卢卡斯定理结果为2的m次幂,m为n的二进制中1的个数。
卢卡斯定理:
【定理】设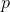 为质数,
为质数,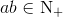 ,且
,且
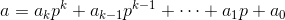 ,
,
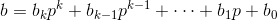 ,
,
其中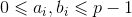 都是整数,
都是整数,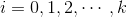 。
。
证明: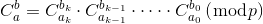 。
。
【推论】当且仅当存在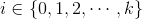 ,使得
,使得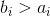 时,
时,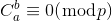 。
。
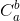 为奇数的充要条件是,在二进制表达下
为奇数的充要条件是,在二进制表达下 的每一个数位上的数都不小于
的每一个数位上的数都不小于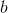 的相应数位上的数。
的相应数位上的数。
其中
证明:
【推论】当且仅当存在
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <map>
#include <string>
#include <stack>
#include <cctype>
#include <vector>
#include <queue>
#include <set>
#include <utility>
using namespace std;
//#define Online_Judge
#define outstars cout << "***********************" << endl;
#define clr(a,b) memset(a,b,sizeof(a))
#define lson l , mid , rt << 1
#define rson mid + 1 , r , rt << 1 | 1
//#define mid ((l + r) >> 1)
#define mk make_pair
#define FOR(i , x , n) for(int i = (x) ; i < (n) ; i++)
#define FORR(i , x , n) for(int i = (x) ; i <= (n) ; i++)
#define REP(i , x , n) for(int i = (x) ; i > (n) ; i--)
#define REPP(i ,x , n) for(int i = (x) ; i >= (n) ; i--)
const int MAXN = 100000000;
const long long LLMAX = 0x7fffffffffffffffLL;
const long long LLMIN = 0x8000000000000000LL;
const int INF = 0x3f3f3f3f;
const int IMIN = 0x80000000;
const double E = 2.718281828;
#define eps 1e-8
#define DEBUG 1
#define mod 100000007
typedef long long LL;
const double PI = acos(-1.0);
typedef double D;
typedef pair<int , int> pi;
// #pragma comment(linker, "/STACK:102400000,102400000")__int64 a[10050];
int c[MAXN];
int cal(int x)
{
int ret = 0;
for(int i = 0; i < 32; i ++) {
if(x & (1<<i)) {
ret ++;
}
if((1 << i) > x) break;
}
return ret;
}
int Pow(int x , int num)
{
int sum = 1;
while(num --)
{
sum *= x;
}
return sum;
}
int main()
{
int n , num;
// cout << (4 & 11) << endl;
//freopen("output.txt" , "w" , stdout );
while(~scanf("%d" , &n))
{
printf("%d\n" ,Pow(2 ,cal(n)));
// c[n] = num;
}
return 0;
}
///printf("%d\n" , (n & 1) ? n + 1 : 2);