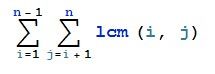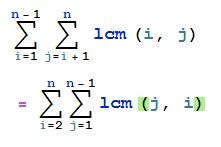Light OJ 1375 LCM Extreme 欧拉函数 (或 莫比乌斯反演 ?)

题目大意：

大意很好理解，就是求和

其中 lcm(i, j) 表示整数 i 和 j 的最小公倍数，结果模上 2^32

大致思路：
这个题和SPOJ 5971很像 可以先看看 SPOJ 5971题解

这答题我们先把需要求的项列出来得到下面这个样子：

lcm(1, 2)   lcm(1, 3)   lcm(1, 4) ....    lcm(1, n)

                   lcm(2, 3)   lcm(2, 4).....    lcm(2, n)

                                      lcm(3, 4).....     lcm(3, n)

                                                     ......    lcm(n - 1, n)

很明显求和式可以转变为：

这样子就很好求了， 每次求出 sigma(lcm( j , k),  1 <= j <= k)之后将结果求和就是要的结果，而且这答题中相比SPOJ 5971来说要简单一点 (少一项特殊的勉强算简单吧)

最终共识SPOJ 5971的题解里写过了~

代码如下：

Result  :  Accepted     Memory  :  60280 KB     Time  :  848 ms

/*
 * Author: Gatevin
 * Created Time:  2014/8/4 13:32:22
 * File Name: test.cpp
 */
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
#include<iomanip>
using namespace std;
const double eps(1e-8);
typedef long long lint;
typedef unsigned long long ulint;

#define maxn 3000010

int phi[maxn];
ulint ans[maxn];
ulint f[maxn];
int t;
int n;

void initial()
{
    memset(phi, 0, sizeof(phi));
    phi[1] = 1;
    for(int i = 2; i < maxn; i++)
    {
        if(!phi[i])
        {
            for(int j = i; j < maxn; j += i)
            {
                if(!phi[j])
                {
                    phi[j] = j;
                }
                phi[j] = phi[j] / i * (i - 1);
            }
        }
    }
    memset(ans, 0, sizeof(ans));
    memset(f, 0, sizeof(f));
    for(int i = 2; i < maxn; i++)
    {
      //  f[i] += i*((ulint)phi[i]) / 2 * i;
      //  ans[i] = ans[i - 1] + f[i];
        for(int j = i; j < maxn; j += i)
        {
            f[j] += ((ulint)phi[i])*i / 2 * j;
        }
        ans[i] = ans[i - 1] + f[i];
    }
    return;
}

int main()
{
    scanf("%d",&t);
    initial();
    for(int cas = 1; cas <= t; cas++)
    {
        scanf("%d", &n);
        printf("Case %d: %llu\n", cas, ans[n]);
    }
    return 0;
}