hdu5120——Intersection

Intersection

Time Limit: 4000/4000 MS (Java/Others)    Memory Limit: 512000/512000 K (Java/Others)
Total Submission(s): 119    Accepted Submission(s): 49

Problem Description

Matt is a big fan of logo design. Recently he falls in love with logo made up by rings. The following figures are some famous examples you may know.


A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.


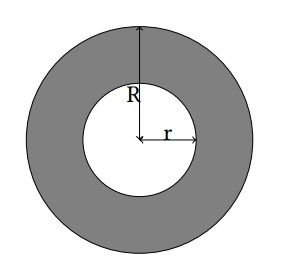
Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.

 

Input

The first line contains only one integer T (T ≤ 10 ⁵), which indicates the number of test cases. For each test case, the first line contains two integers r, R (0 ≤ r < R ≤ 10).

Each of the following two lines contains two integers x _i, y _i (0 ≤ x _i, y _i ≤ 20) indicating the coordinates of the center of each ring.

 

Output

For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the area of intersection rounded to 6 decimal places.

 

Sample Input

   
   
   
   

    
    
    
    2
2 3
0 0
0 0
2 3
0 0
5 0
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    Case #1: 15.707963
Case #2: 2.250778
   
   
   
   

 

Source

2014ACM/ICPC亚洲区北京站-重现赛（感谢北师和上交）

 

Recommend

圆环相交 --->大圆交大圆（如果相交） - 2 * 大圆交小圆 （如果相交） + 小圆交小圆（如果相交）

重现赛不知道哪里写错了一直WA，赛后推翻重写就AC了

#include <map>
#include <set>
#include <list>
#include <queue>
#include <stack>
#include <vector>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const double pi = acos(-1);
struct point
{
	double x, y;
};

double calc_area(point a, point b, double r1, double r2)
{
	double d = sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
	if (r1 - r2 - d >= 0)
	{
		return pi * r2 * r2;
	}
	double ang1 = acos((r1 * r1 + d * d - r2 * r2) / (2 * r1 * d));
	double ang2 = acos((r2 * r2 + d * d - r1 * r1) / (2 * r2 * d));
	return ang1 * r1 * r1 + ang2 * r2 * r2 - 0.5 * r1 * d * sin(ang1) - 0.5 * r2 * d * sin(ang2);
}

int main()
{
	int t, icase = 1;
	scanf("%d", &t);
	while (t--)
	{
		double r, R, ans = 0;
		point p1, p2;
		scanf("%lf%lf", &r, &R);
		scanf("%lf%lf", &p1.x, &p1.y);
		scanf("%lf%lf", &p2.x, &p2.y);
		double d = sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
		printf("Case #%d: ", icase++);
		if (d >= (2 * R))
		{
			printf("0.000000\n");
			continue;
		}
		ans = calc_area(p1, p2, R, R);
		if (d >= (R + r))
		{
			printf("%f\n", ans);
			continue;
		}
		ans -= 2 * calc_area(p1, p2, R, r);
		if (d >= (2 * r))
		{
			printf("%f\n", ans);
			continue;
		}
		ans += calc_area(p1, p2, r, r);
		printf("%f\n", ans);
	}
	return 0;
}