Codeforces #283 Div 1 简要题解

比赛总结

算了不提了，比赛时只弄出来第一题，wa了7次，罚时跪得一塌糊涂，*了狗了。。。

A. Removing Columns

题目链接

http://codeforces.com/contest/497/problem/A

题目大意

给你 n 个依次排列的长度为 m 的字符串，构成一个 n∗m 大小的表格，每次你从中删除一列。问最少删除多少次，才能使得这些字符串是字典序的

思路

非常坑爹的细节题，其间不知道wa了多少次。。。。

显然是个贪心，我们从第一列到最后一列扫，只要能保留的列，保留下来肯定对后面没有影响。

如果当前在保留下来的列中，某些字符串的前缀都一样：
AAAAAA?…..
AAAAAA?…..
…….
AAAAAA?…..
那么?列就必须得按照字母非降排序，类似下面这样
AAAAAA A…..
AAAAAA B…..
…….
AAAAAA E…..

否则这一列随便什么顺序都行

我们可以维护一个数组 mark[i] ， mark[i]=true 表示在保留下来的列中，第 i 个字符串和第 i+1 个字符串的前缀相同。显然扫到某一列时，若 mark[i]=true ，但是这一列的第 i 行字母大于 i+1 行的字母，则这一列显然不能要，可以发现，如果这一列存在 i,j(j>i) ，且第 i 行字母大于 j 行的字母，也存在 i′ ，使得这一列的第 i′ 行字母大于 i′+1 行的字母。其他情况下这一列可以保留

代码

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>

#define MAXN 510

using namespace std;

char mp[MAXN][MAXN];
int n,m,maxans=0;
bool mark[MAXN];

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%s",mp[i]+1);
    int ans=0;
    for(int j=1;j<=m;j++)
    {
        bool flag=true;
        for(int i=1;i<n;i++)
        {
            if(!mark[i]&&mp[i][j]>mp[i+1][j])
            {
                ans++;
                flag=false;
                break;
            }
        }
        if(flag)
        {
            for(int i=1;i<n;i++)
                if(mp[i][j]<mp[i+1][j])
                    mark[i]=true;
        }
    }
    printf("%d\n",ans);
    return 0;
}

B. Tennis Game

题目链接

http://codeforces.com/contest/497/problem/B

题目大意

A和B打 n 次羽毛球，给出每一次的胜负情况(1:A胜 2:B胜)，一个人在这个游戏中胜利需要满足两个条件：1、每一局最先赢 t 个球 2、最先赢 s 局。如果已经可以确定胜负，则比赛终止。输出所有可能的合法 (s,t) 组合。

思路

首先我们枚举 t ，然后看是否能正好打完 n 次羽毛球并确定胜负。我们可以不断地二分到了什么时候，A和B中有一个人赢得了新的一局。然后记录下A和B各自赢得的局数 totA,totB ，如此反复，若恰好用完了 n 次回合，且 totA 和 totB 不相等，而且赢了 maxtotA,totB 局的那一方也恰好赢得了第 n 次羽毛球(如果胜利者没有赢得第n局，显然是不科学的)，那么就能得到一个合法的 (s,t) 组合

代码

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <vector>

#define MAXN 210000

using namespace std;

int n;
int result[MAXN];
int sumA[MAXN],sumB[MAXN];

vector<pair<int,int> >sol;

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&result[i]);
    for(int i=1;i<=n;i++)
    {
        sumA[i]=sumA[i-1]+(result[i]==1);
        sumB[i]=sumB[i-1]+(result[i]==2);
    }
    for(int t=1;t<=n;t++)
    {
        int totA=0,totB=0,p=0;
        while(p<n)
        {
            int lowerBound=p+1,upperBound=n,ans=-1;
            while(lowerBound<=upperBound)
            {
                int mid=(lowerBound+upperBound)>>1;
                if(sumA[mid]-sumA[p]>=t||sumB[mid]-sumB[p]>=t)
                {
                    ans=mid;
                    upperBound=mid-1;
                }
                else lowerBound=mid+1;
            }
            if(ans==-1) break;
            if(sumA[ans]-sumA[p]>=t&&sumB[ans]-sumB[p]<t) totA++;
            if(sumA[ans]-sumA[p]<t&&sumB[ans]-sumB[p]>=t) totB++;
            if(ans==n&&totA!=totB)
            {
                if(totA>totB&&result[ans]!=1) break;
                if(totA<totB&&result[ans]!=2) break;
                sol.push_back(make_pair(max(totA,totB),t));
            }
            p=ans;
        }
    }
    sort(sol.begin(),sol.end());
    printf("%d\n",sol.size());
    for(int i=0;i<sol.size();i++)
        printf("%d %d\n",sol[i].first,sol[i].second);
    return 0;
}

C. Distributing Parts

题目链接

http://codeforces.com/contest/497/problem/C

题目大意

给你 n 个红色线段 [Li,Ri] ,以及 m 个蓝色线段 [L′i,R′i] ，一个蓝色线段 [L′i,R′i] 能覆盖一个红色线段 [Li,Ri] ，当且仅当 L′i≤Li≤Ri≤R′i ，且一个蓝色线段可以覆盖 ki 个不同的红色线段，问是否能用蓝色线段覆盖掉所有的红色线段，并输出一种可行方案。

思路

比较简单的贪心。我们首先将红色线段和蓝色线段按照第一关键字右端点升序、第二关键字左端点升序来排序，然后从左到右扫蓝色线段 i ，每次在set里加入右端点 ≤Ri 的红色线段。这样的话，我们就可以不必考虑右端点的影响，而且set里保存的是没有被删除的、且右端点 ≤Ri 的红色线段。然后我们在set里lowerbound出 Lj>=Li 的最小的红色线段j，并在set里删去它。如此做 ki 次直到找不出这样的红色线段为止。显然这样的贪心是正确的，能覆盖最多的红色线段。

代码

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
#include <vector>
#include <set>

#define MAXN 210000

using namespace std;

int n,m;

struct Segment
{
    int L,R,k,id;
}song[MAXN],musician[MAXN];

bool operator<(Segment a,Segment b)
{
    if(a.R==b.R)
        return a.L<b.L;
    return a.R<b.R;
}

int belong[MAXN];

struct Info
{
    int L,R,id;
    Info(){}
    Info(int _L,int _R,int _id):L(_L),R(_R),id(_id){}
};

bool operator<(Info a,Info b)
{
    if(a.L==b.L) return a.R<b.R;
    return a.L<b.L;
}

bool operator>(Info a,Info b)
{
    if(a.L==b.L)
        return a.R>b.R;
    return a.L>b.L;
}

multiset<Info>bst; //!!!
multiset<Info>::iterator it;

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&song[i].L,&song[i].R);
        song[i].id=i;
    }
    scanf("%d",&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d%d",&musician[i].L,&musician[i].R,&musician[i].k);
        musician[i].id=i;
    }
    sort(song+1,song+n+1);
    sort(musician+1,musician+m+1);
    int p=1,tot=0; //tot=被演奏的歌曲个数
    for(int i=1;i<=m;i++)
    {
        for(;p<=n&&song[p].R<=musician[i].R;p++)
        {
            //cout<<"L:"<<song[p].L<<" R:"<<song[p].R<<endl;
            bst.insert(Info(song[p].L,song[p].R,song[p].id));
        }
        for(int t=1;t<=musician[i].k;t++)
        {
            it=bst.lower_bound(Info(musician[i].L,0,0));
            if(it==bst.end()) break;
            belong[it->id]=musician[i].id;
            bst.erase(it);
            tot++;
        }
    }
    if(tot!=n)
    {
        printf("NO\n");
        return 0;
    }
    printf("YES\n");
    for(int i=1;i<=n;i++)
        printf("%d ",belong[i]);
    printf("\n");
    return 0;
}

D. Gears

题目链接

http://codeforces.com/contest/497/problem/D

题目大意

给你两个多边形，每个多边形会以一个点为中心顺时针旋转。两个多边形旋转的速度(rad/s)相同，每个多边形各有一个旋转中心。
问这两个多边形旋转过程中是否会发生碰撞

思路

观察发现，碰撞发生时，肯定是一个多边形的顶点撞上了另一个多边形的边。不妨设多边形B的顶点撞上了多边形A的边（多边形A的顶点撞上了多边形B的边的情况，只需要把A和B对换一下就行了）。我们不妨固定多边形A不动，让B绕着A做逆时针公转，自己做顺时针自转，公转和自转的速率相同。

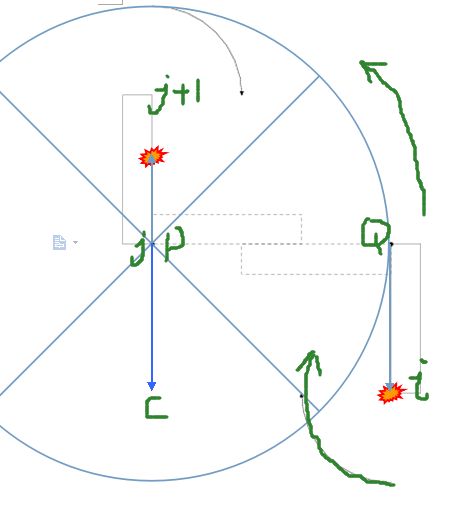
如上图，设多边形A的旋转中心为P，B的中心为Q。则B公转的轨道就是图上蓝色的、以P为圆心、半径为PQ的圆。设黄色点 Bi 为碰撞点，得到 C 点， C=P+QBi→ 。若点 C 到线段 AjAj+1 的距离小于等于 PQ ，且并不是线段 AjAj+1 上所有的点到点 C 的距离小于等于 PQ ，则A的边 AjAj+1 和B的点 Bi 会发生碰撞。并不是很好证明，不过自己多画几个图可能就比较好理解了。

代码

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>

#define MAXN 1100

using namespace std;

typedef long long int LL;

struct Point
{
    LL x,y;
    Point(){}
    Point(LL _x,LL _y):x(_x),y(_y){}
}pA[MAXN],pB[MAXN],centerA,centerB;

int n,m;

Point operator-(Point a,Point b)
{
    return Point(a.x-b.x,a.y-b.y);
}

Point operator+(Point a,Point b)
{
    return Point(a.x+b.x,a.y+b.y);
}

LL cross(Point a,Point b)
{
    return a.x*b.y-a.y*b.x;
}

LL dist(Point a,Point b)
{
    return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);
}

struct Line
{
    Point st,ed;
    Line(){}
    Line(Point _st,Point _ed):st(_st),ed(_ed){}
};

bool check() //为了防止被坑爹卡精度，所有的距离全部是实际距离的平方，面积也得是平方
{
    LL R=dist(centerA,centerB); //公转轨道的圆的半径
    for(int i=1;i<=m;i++) //枚举B上的点i落到了A上面
    {
        Point tmpC=centerA+(pB[i]-centerB);
        for(int j=1;j<=n;j++) //枚举A上的边j->j+1
        {
            Point tmpA=pA[j],tmpB=pA[j%n+1];
            LL disA=dist(tmpA,tmpC),disB=dist(tmpB,tmpC);
            if(disA-R<=0&&disB-R>=0) //disA和disB中一个比R大，一个比R小，表明A上的边j->j+1会碰撞上B上的点i
                return true;
            if(disA-R>=0&&disB-R<=0) //disA和disB中一个比R大，一个比R小，表明A上的边j->j+1会碰撞上B上的点i
                return true;
            //if(disA-R<0&&disB-R<0) continue;
            if(max(disA,disB)*2>disA+disB+dist(tmpA,tmpB)) continue;
            if(cross(tmpC-tmpA,tmpB-tmpA)*cross(tmpC-tmpA,tmpB-tmpA)<=R*dist(tmpA,tmpB)&&disA>=R) //!!!!B上的点i到边j->j+1的距离小于等于R
                return true;
        }
    }
    return false;
}

int main()
{
    scanf("%I64d%I64d",&centerA.x,&centerA.y);
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%I64d%I64d",&pA[i].x,&pA[i].y);

    scanf("%I64d%I64d",&centerB.x,&centerB.y);
    scanf("%d",&m);
    for(int i=1;i<=m;i++) scanf("%I64d%I64d",&pB[i].x,&pB[i].y);

    if(check())
    {
        printf("YES\n");
        return 0;
    }

    swap(n,m);
    swap(centerA,centerB);
    swap(pA,pB);

    if(check())
    {
        printf("YES\n");
        return 0;
    }

    printf("NO\n");
    return 0;
}