目标检测之harr特征
目标检测的图像特征提取之(三)Haar特征
http://blog.csdn.net/zouxy09
1、Haar-like特征
Haar-like特征最早是由Papageorgiou等应用于人脸表示,Viola和Jones在此基础上,使用3种类型4种形式的特征。
Haar特征分为三类:边缘特征、线性特征、中心特征和对角线特征,组合成特征模板。特征模板内有白色和黑色两种矩形,并定义该模板的特征值为白色矩形像素和减去黑色矩形像素和。Haar特征值反映了图像的灰度变化情况。例如:脸部的一些特征能由矩形特征简单的描述,如:眼睛要比脸颊颜色要深,鼻梁两侧比鼻梁颜色要深,嘴巴比周围颜色要深等。但矩形特征只对一些简单的图形结构,如边缘、线段较敏感,所以只能描述特定走向(水平、垂直、对角)的结构。
对于图中的A, B和D这类特征,特征数值计算公式为:v=Sum白-Sum黑,而对于C来说,计算公式如下:v=Sum白-2*Sum黑;之所以将黑色区域像素和乘以2,是为了使两种矩形区域中像素数目一致。
通过改变特征模板的大小和位置,可在图像子窗口中穷举出大量的特征。上图的特征模板称为“特征原型”;特征原型在图像子窗口中扩展(平移伸缩)得到的特征称为“矩形特征”;矩形特征的值称为“特征值”。
矩形特征可位于图像任意位置,大小也可以任意改变,所以矩形特征值是矩形模版类别、矩形位置和矩形大小这三个因素的函数。故类别、大小和位置的变化,使得很小的检测窗口含有非常多的矩形特征,如:在24*24像素大小的检测窗口内矩形特征数量可以达到16万个。这样就有两个问题需要解决了:(1)如何快速计算那么多的特征?---积分图大显神通;(2)哪些矩形特征才是对分类器分类最有效的?---如通过AdaBoost算法来训练(这一块这里不讨论,具体见http://blog.csdn.net/zouxy09/article/details/7922923)
2、Haar-like特征的计算—积分图
积分图就是只遍历一次图像就可以求出图像中所有区域像素和的快速算法,大大的提高了图像特征值计算的效率。
积分图主要的思想是将图像从起点开始到各个点所形成的矩形区域像素之和作为一个数组的元素保存在内存中,当要计算某个区域的像素和时可以直接索引数组的元素,不用重新计算这个区域的像素和,从而加快了计算(这有个相应的称呼,叫做动态规划算法)。积分图能够在多种尺度下,使用相同的时间(常数时间)来计算不同的特征,因此大大提高了检测速度。
我们来看看它是怎么做到的。
积分图是一种能够描述全局信息的矩阵表示方法。积分图的构造方式是位置(i,j)处的值ii(i,j)是原图像(i,j)左上角方向所有像素的和:
积分图构建算法:
1)用s(i,j)表示行方向的累加和,初始化s(i,-1)=0;
2)用ii(i,j)表示一个积分图像,初始化ii(-1,i)=0;
3)逐行扫描图像,递归计算每个像素(i,j)行方向的累加和s(i,j)和积分图像ii(i,j)的值
s(i,j)=s(i,j-1)+f(i,j)
ii(i,j)=ii(i-1,j)+s(i,j)
4)扫描图像一遍,当到达图像右下角像素时,积分图像ii就构造好了。
积分图构造好之后,图像中任何矩阵区域的像素累加和都可以通过简单运算得到如图所示。
设D的四个顶点分别为α、β、γ、δ,则D的像素和可以表示为
Dsum = ii( α )+ii( β)-(ii( γ)+ii( δ ));
而Haar-like特征值无非就是两个矩阵像素和的差,同样可以在常数时间内完成。所以矩形特征的特征值计算,只与此特征矩形的端点的积分图有关,所以不管此特征矩形的尺度变换如何,特征值的计算所消耗的时间都是常量。这样只要遍历图像一次,就可以求得所有子窗口的特征值。
3、Haar-like矩形特征拓展
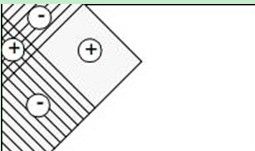
Lienhart R.等对Haar-like矩形特征库作了进一步扩展,加入了旋转45。角的矩形特征。扩展后的特征大致分为4种类型:边缘特征、线特征环、中心环绕特征和对角线特征:
在特征值的计算过程中,黑色区域的权值为负值,白色区域的权值为正值。而且权值与矩形面积成反比(使两种矩形区域中像素数目一致);
竖直矩阵特征值计算:
对于竖直矩阵,与上面2处说的一样。
45°旋角的矩形特征计算:
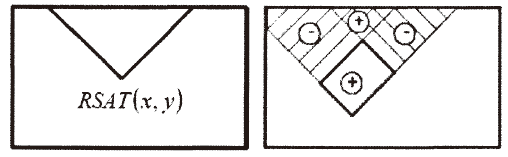
对于45°旋角的矩形,我们定义RSAT(x,y)为点(x,y)左上角45°区域和左下角45°区域的像素和。
用公式可以表示为:
为了节约时间,减少重复计算,可按如下递推公式计算:
而计算矩阵特征的特征值,是位于十字行矩形RSAT(x,y)之差。可参考下图:
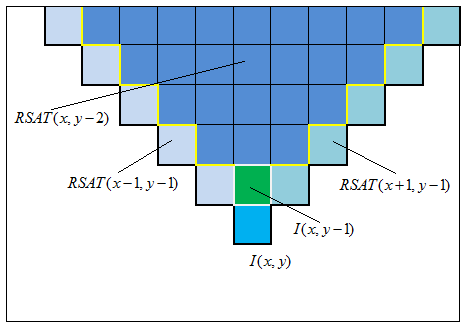
构造旋转积分图像Rotated SummedArea Table
旋转积分图中,每个点存储是其左上方延伸出的45°区域范围内所有像素之和:
RSAT(x,y)也采用增量方计算得到:
![]()
初始边界:RSAT(-1,y)=RSAT(x,-1)=RSAT(x,-2)=0
RSAT(-1,-1)=RSAT(-1,-2)=0
公式具体示意如下图:
计算Haar矩形特征
同样的方式,可推出每个矩形内像素和的计算公式:
同样的,无论旋转矩形r的尺寸大小,只需要查找积分图像4次就可以求得任意矩形内像素值得和。