hdu 3480 Division (斜率优化||四边形不等式)
Division
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 999999/400000 K (Java/Others)
Total Submission(s): 2676 Accepted Submission(s): 1056
Problem Description
Little D is really interested in the theorem of sets recently. There’s a problem that confused him a long time.
Let T be a set of integers. Let the MIN be the minimum integer in T and MAX be the maximum, then the cost of set T if defined as (MAX – MIN)^2. Now given an integer set S, we want to find out M subsets S1, S2, …, SM of S, such that
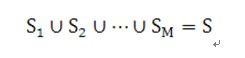
and the total cost of each subset is minimal.
Let T be a set of integers. Let the MIN be the minimum integer in T and MAX be the maximum, then the cost of set T if defined as (MAX – MIN)^2. Now given an integer set S, we want to find out M subsets S1, S2, …, SM of S, such that
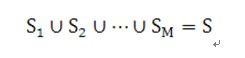
and the total cost of each subset is minimal.
Input
The input contains multiple test cases.
In the first line of the input there’s an integer T which is the number of test cases. Then the description of T test cases will be given.
For any test case, the first line contains two integers N (≤ 10,000) and M (≤ 5,000). N is the number of elements in S (may be duplicated). M is the number of subsets that we want to get. In the next line, there will be N integers giving set S.
In the first line of the input there’s an integer T which is the number of test cases. Then the description of T test cases will be given.
For any test case, the first line contains two integers N (≤ 10,000) and M (≤ 5,000). N is the number of elements in S (may be duplicated). M is the number of subsets that we want to get. In the next line, there will be N integers giving set S.
Output
For each test case, output one line containing exactly one integer, the minimal total cost. Take a look at the sample output for format.
Sample Input
2 3 2 1 2 4 4 2 4 7 10 1
Sample Output
Case 1: 1 Case 2: 18HintThe answer will fit into a 32-bit signed integer.
Source
2010 ACM-ICPC Multi-University Training Contest(5)——Host by BJTU
题意:
将含有N个元素的一个集合分成M个子集,使得每个子集的最大值与最小值平方差的和最小。
思路1:
(斜率优化)
可以想到贪心将元素从小到大排序,很快可以得出dp[i][j]-前i个子集分j个元素的最小花费,
dp方程 dp[i][j]=dp[i-1][k]+(a[j]-a[k+1]);
但是需要三重循环,时间复杂度接受不了,所以需要优化,这题斜率优化和四边形不等式都可以,先看斜率优化。
设k1<k2<j,如果k1比k2优,则有dp[i-1][k1]+(a[j]-a[k1+1])^2<dp[i-1][k2]+(a[j]-a[k2+1])^2;
化简得 ( dp[i-1][k1]+a[k1+1]^2-(dp[i-1][k2]+a[k2+1]^2) )/(a[k1+1]-a[k2+1])<=2a[j];
类比斜率,可以得出
y:dp[i-1][k1]+a[k1+1]^2;
x: a[k1+1];
于是和之前见到的斜率优化有了一个相同的式子 (y1-y2)/(x1-x2)<k;于是可以用一个单调队列来维护一个下凸函数优化dp了。
斜率优化可以用滚动数组实现,节约内存一些。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <stack>
#include <vector>
#include <set>
#include <queue>
#define maxn 205
#define MAXN 100005
#define mod 100000000
#define INF 0x3f3f3f3f
#define pi acos(-1.0)
#define eps 1e-6
typedef long long ll;
using namespace std;
int n,m,ans,cnt,tot,flag;
int a[10005],dp[2][10005];
int q[10005];
int sqr(int x)
{
return x*x;
}
int get(int i,int k)
{
return dp[i][k]+a[k+1]*a[k+1];
}
void solve()
{
int i,j,t,dx1,dy1,dx2,dy2,k1,k2,turn=0;
int head,tail;
sort(a+1,a+n+1);
memset(dp,0x3f,sizeof(dp));
dp[0][0]=0;
for(i=1; i<=m; i++)
{
head=0; tail=-1;
q[++tail]=i-1;
for(j=i; j<=n; j++)
{
while(head<tail) // 将不再更新答案的点删除
{
k1=q[head+1];
k2=q[head];
dx1=a[k1+1]-a[k2+1];
dy1=get(turn,k1)-get(turn,k2);
if(dy1<=dx1*2*a[j]) head++;
else break ;
}
dp[turn^1][j]=dp[turn][q[head]]+sqr(a[j]-a[q[head]+1]);
while(head<tail) // 维护下凸曲线
{
dx1=a[j+1]-a[q[tail]+1];
dy1=get(turn,j)-get(turn,q[tail]);
dx2=a[q[tail]+1]-a[q[tail-1]+1];
dy2=get(turn,q[tail])-get(turn,q[tail-1]);
if(dy1*dx2<=dy2*dx1) tail--;
else break ;
}
q[++tail]=j;
}
turn^=1;
}
ans=dp[turn][n];
}
int main()
{
int i,j,t,test=0;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&m);
for(i=1; i<=n; i++)
{
scanf("%d",&a[i]);
}
solve();
printf("Case %d: %d\n",++test,ans);
}
return 0;
}
思路来源于:Staginner
有关四边形不等式的证明见赵爽的论文。
dp[i][j]=dp[i-1][k-1]+w[k][j],由于w[i+1][j]-w[i][j]=(a[i]-a[i+1])*(2*a[j]-a[i+1]-a[i]),这个表达式是随着j的增加单调递减的,所以就有w[i+1][j+1]-w[i][j+1]<=w[i+1][j]-w[i][j],也就是w[i][j]+w[i+1][j+1]<=w[i][j+1]+w[i+1][j],满足四边形不等式优化的条件,我们就可以放心地使用四边形不等式优化dp了。
对于dp[i][j]的决策s[i][j],有s[i][j-1]<=s[i][j]<=s[i+1][j],在dp[i][j]求出来之前要先求出dp[i][j-1]、dp[i+1][j],可以按照长度递增来递推,具体见代码,还有注意初始化。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <stack>
#include <vector>
#include <set>
#include <queue>
#define maxn 205
#define MAXN 100005
#define mod 100000000
#define INF 0x3f3f3f3f
#define pi acos(-1.0)
#define eps 1e-6
typedef long long ll;
using namespace std;
int n,m,ans,cnt,tot,flag;
int a[10005],dp[5005][10005],s[5005][10005];
void solve()
{
int i,j,k,t;
memset(dp,0x3f,sizeof(dp));
for(i=0;i<=m;i++)
{
dp[i][i]=0;
s[i][i]=i;
}
for(i=m+1;i<=n;i++)
{
s[m+1][i]=i;
}
for(int len=1;len<n;len++)
{
for(i=1;i<=m;i++)
{
j=i+len;
if(j>n) break ;
for(k=s[i][j-1];k<=s[i+1][j];k++)
{
t=dp[i-1][k-1]+(a[k]-a[j])*(a[k]-a[j]);
if(dp[i][j]>t)
{
dp[i][j]=t; s[i][j]=k;
}
}
}
}
ans=dp[m][n];
}
int main()
{
int i,j,t,test=0;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&m);
for(i=1; i<=n; i++)
{
scanf("%d",&a[i]);
}
sort(a+1,a+n+1);
solve();
printf("Case %d: %d\n",++test,ans);
}
return 0;
}