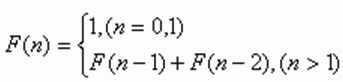HITOJ 2060 类似斐波那契数列（一段和取模）

http://acm.hit.edu.cn/hoj/problem/view?id=2060

As we know , the Fibonacci numbers are defined as follows:

 """"

Given two numbers a and b , calculate . """"

Input

The input contains several test cases. Each test case consists of two non-negative integer numbers a and b (0 ≤ a ≤ b ≤1,000,000,000). Input is terminated by a = b = 0.

Output

For each test case, output S mod 1,000,000,000, since S may be quite large.

Sample Input

1 1
3 5
10 1000
0 0

Sample Output

1
16
496035733

题目大意：给一个类似于Fibonacci的数列，求第a项到第b项的和取模。

解题思路：构造一个3*3的矩阵，利用矩阵连乘的思想求解

/*This Code is Submitted by life4711 for Problem 2060 at 2014-07-25 14:52:17*/
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <math.h>
using namespace std;
typedef long long LL;
const int N=3;
const LL MOD=1000000000;
struct Matrix
{
    LL m[N][N];
};
Matrix I=
{
    1,0,0,
    0,1,0,
    0,0,1
};
Matrix multi(Matrix a,Matrix b)
{
    Matrix c;
    for(int i=0; i<N; i++)
        for(int j=0; j<N; j++)
        {
            c.m[i][j]=0;
            for(int k=0; k<N; k++)
            {
                c.m[i][j]+=a.m[i][k]*b.m[k][j]%MOD;
            }
            c.m[i][j]=c.m[i][j]%MOD;
        }
    return c;
}
Matrix quick_mod(Matrix a,LL k)
{
    Matrix ans=I;
    while(k!=0)
    {
        if(k&1)
        {
            ans=multi(ans,a);
        }
        k>>=1;
        a=multi(a,a);
    }
    return ans;
}
int main()
{
    LL n,m;
    while(~scanf("%lld%lld",&n,&m))
    {
        if(n==0&&m==0)
            break;
        Matrix A={1,1,1,
                  0,1,1,
                  0,1,0};

        if(n==0)
        {
            Matrix x1=quick_mod(A,m-1);
            LL s=(x1.m[0][0]*2%MOD+x1.m[0][1]+x1.m[0][2])%MOD;
            if(s<0)
                s+=MOD;
            printf("%lld\n",s);
        }
        else if(n==1)
        {
            Matrix x1=quick_mod(A,m-1);
            LL s=(x1.m[0][0]*2%MOD+x1.m[0][1]+x1.m[0][2])%MOD;
            s=(s-1)%MOD;
            if(s<0)
                s+=MOD;
            printf("%lld\n",s);
        }
        else
        {
            Matrix x1=quick_mod(A,m-1);
            LL s1=(x1.m[0][0]*2%MOD+x1.m[0][1]+x1.m[0][2])%MOD;
            x1=quick_mod(A,n-2);
            LL s2=(x1.m[0][0]*2%MOD+x1.m[0][1]+x1.m[0][2])%MOD;
            s1=(s1%MOD-s2%MOD)%MOD;
            if(s1<0)
                s1+=MOD;
            printf("%lld\n",s1);
        }
    }
    return 0;
}