ZOJ 2158/POJ 1789 - Truck History

最小生成树 - Prim算法

 

 

题意：有n辆卡车，卡车的编号由7为小写字母的字符串组成，优劣值的计算方法是：将卡车类型编号的距离定义成卡车类型编码字符串中（7个位置上）不同字符串的位置数目（这里可能很多人看不懂题目什么意思）。

 

分析：其中提到的派生方案的优劣值：1/Σ_(to,td)d(t_o,t_d)，要使优劣值最大，即分母Σ_(to,td)d(t_o,t_d)最小。另外，要求考虑到所有类型对（t0 , td）的距离，使得最终派生方案中每种卡车类型都是由其他一种卡车类型派生出来的（最初代的卡车类型除外）。这样，如果将每种卡车的类型理解成一个无向网中的顶点，所要求的最佳派生方案就是一颗最小生成树，而Σ_(to,td)d(t_o,t_d)就是最小生成树的权值。

 

例如输入样例中的：

4

aaaaaaa

baaaaaa

abaaaaa

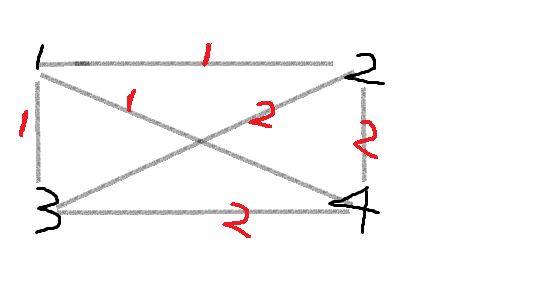
aabaaaa      就可以表示成：

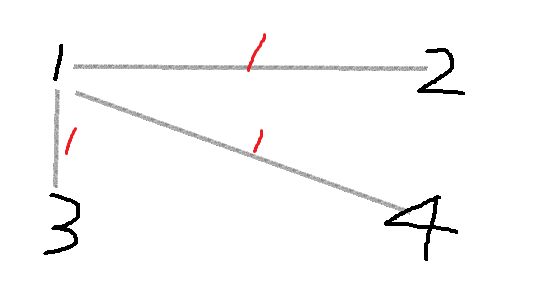
构造成最小生成树就是：

 

 

 

AC代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAXN 2005
#define LEN 10

const int max = 0x7ffffff;
int map[MAXN][MAXN], v[MAXN], low[MAXN];
char code[MAXN][LEN];
int n;

int MinTree()
{
    int i,j,sum,min,flag;
    memset(low, 0, sizeof(low));
    memset(v, 0, sizeof(v));
    v[1] = 1;
    sum = 0;
    for(j=2; j<=n; j++)
    {
        low[j] = map[1][j];
    }
    for(i=2; i<=n; i++)
    {
        min = max;
        flag = -1;
        for(j=1; j<=n; j++)
        {
            if(!v[j] && low[j]<min)
            {
                min = low[j];
                flag = j;
            }
        }
        sum += min;
        v[flag] = 1;
        for(j=1; j<=n; j++)
        {
            if(!v[j] && map[flag][j]<low[j])
            {
                low[j] = map[flag][j];
            }
        }
    }
    return sum;
}

int main()
{
    int i,j,k,dis;
    while(scanf("%d",&n),n)
    {
        for(i=1; i<=n; i++)
            for(j=1; j<=n; j++)
            {
                if(i==j) map[i][j] = 0;
                else map[i][j] = max;
            }

        for(i=1; i<=n; i++)
        {
            scanf("%s",&code[i]);
            for(j=1; j<=i; j++)  //求第i类型与第j类型编码之间的距离
            {
                dis = 0;
                for(k=0; k<7; k++)
                {
                    if(code[i][k] != code[j][k])
                        dis++;
                }
                map[i][j] = map[j][i] = dis;
            }
        }
        printf("The highest possible quality is 1/%d.\n",MinTree());
    }
    return 0;
}