最短路径之Dijkstra算法详细讲解
转自:http://2728green-rock.blog.163.com/blog/static/43636790200901211848284/
1 最短路径算法
在日常生活中,我们如果需要常常往返A地区和B地区之间,我们最希望知道的可能是从A地区到B地区间的众多路径中,那一条路径的路途最短。最短路径问题是图论研究中的一个经典算法问题, 旨在寻找图(由结点和路径组成的)中两结点之间的最短路径。 算法具体的形式包括:
(1)确定起点的最短路径问题:即已知起始结点,求最短路径的问题。
(2)确定终点的最短路径问题:与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题。在无向图中该问题与确定起点的问题完全等同,在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
(3)确定起点终点的最短路径问题:即已知起点和终点,求两结点之间的最短路径。
(4)全局最短路径问题:求图中所有的最短路径。
用于解决最短路径问题的算法被称做“最短路径算法”, 有时被简称作“路径算法”。 最常用的路径算法有:Dijkstra算法、A*算法、Bellman-Ford算法、Floyd-Warshall算法、Johnson算法。
本文主要研究Dijkstra算法的单源算法。
2 Dijkstra算法
2.1 Dijkstra算法
Dijkstra算法是典型最短路算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
Dijkstra算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
2.2 Dijkstra算法思想
Dijkstra算法思想为:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将 加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2.3 Dijkstra算法具体步骤
(1)初始时,S只包含源点,即S=,v的距离为0。U包含除v外的其他顶点,U中顶点u距离为边上的权(若v与u有边)或 )(若u不是v的出边邻接点)。
(2)从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
(3)以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u(u U)的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
(4)重复步骤(2)和(3)直到所有顶点都包含在S中。
2.4 Dijkstra算法举例说明
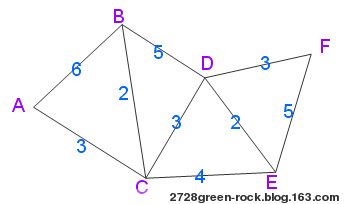
如下图,设A为源点,求A到其他各顶点(B、C、D、E、F)的最短路径。线上所标注为相邻线段之间的距离,即权值。(注:此图为随意所画,其相邻顶点间的距离与图中的目视长度不能一一对等)
图一:Dijkstra无向图
算法执行步骤如下表:【注:图片要是看不到请到“相册--日志相册”中,名为“Dijkstra算法过程”的图就是了】
参考文献
[1] 黄国瑜、叶乃菁,数据结构,清华大学出版社,2001年8月第1版
[2] 最短路径,http://baike.baidu.com/view/349189.htm?func=retitle
[3] 李春葆,数据结构教程,清华大学出版社,2005年1月第1版
[3] Dijkstra算法,http://baike.baidu.com/view/7839.htm