The Last Ant（模拟）

题目链接：http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=1336

Problem B: The Last Ant

A straight tunnel without branches is crowded with busy ants coming and going. Some ants walk left to right and others right to left. All ants walk at a constant speed of 1 cm/s. When two ants meet, they try to pass each other. However, some sections of the tunnel are narrow and two ants cannot pass each other. When two ants meet at a narrow section, they turn around and start walking in the opposite directions. When an ant reaches either end of the tunnel, it leaves the tunnel.

The tunnel has an integer length in centimeters. Every narrow section of the tunnel is integer centimeters distant from the both ends. Except for these sections, the tunnel is wide enough for ants to pass each other. All ants start walking at distinct narrow sections. No ants will newly enter the tunnel. Consequently, all the ants in the tunnel will eventually leave it. Your task is to write a program that tells which is the last ant to leave the tunnel and when it will.

Figure B.1 shows the movements of the ants during the first two seconds in a tunnel 6 centimeters long. Initially, three ants, numbered 1, 2, and 3, start walking at narrow sections, 1, 2, and 5 centimeters distant from the left end, respectively. After 0.5 seconds, the ants 1 and 2 meet at a wide section, and they pass each other. Two seconds after the start, the ants 1 and 3 meet at a narrow section, and they turn around.

Figure B.1 corresponds to the first dataset of the sample input.

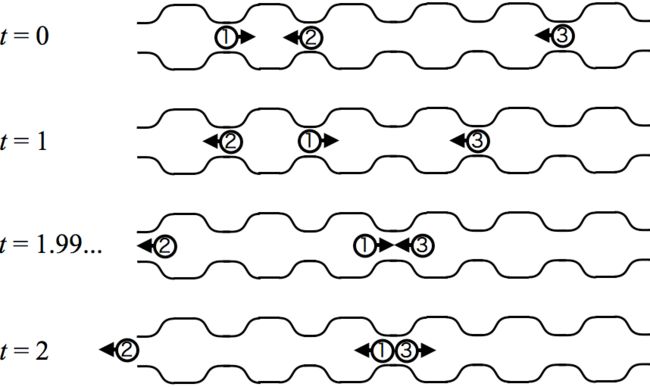
Figure B.1. Movements of ants

Input

The input consists of one or more datasets. Each dataset is formatted as follows.

n l
d1 p1
d2 p2
...
dn pn

The first line of a dataset contains two integers separated by a space. n (1 ≤ n ≤ 20) represents the number of ants, and l (n + 1 ≤ l ≤ 100) represents the length of the tunnel in centimeters. The following n lines describe the initial states of ants. Each of the lines has two items, di and pi, separated by a space. Ants are given numbers 1 through n. The ant numbered i has the initial direction di and the initial position pi. The initial direction di (1 ≤ i ≤ n) is L (to the left) or R (to the right). The initial position pi (1 ≤ i ≤ n) is an integer specifying the distance from the left end of the tunnel in centimeters. Ants are listed in the left to right order, that is, 1 ≤ p1 < p2 < ... < pn ≤ l - 1.

The last dataset is followed by a line containing two zeros separated by a space.

Output

For each dataset, output how many seconds it will take before all the ants leave the tunnel, and which of the ants will be the last. The last ant is identified by its number. If two ants will leave at the same time, output the number indicating the ant that will leave through the left end of the tunnel.

Sample Input

3 6
R 1
L 2
L 5
1 10
R 1
2 10
R 5
L 7
2 10
R 3
L 8
2 99
R 1
L 98
4 10
L 1
R 2
L 8
R 9
6 10
R 2
R 3
L 4
R 6
L 7
L 8
0 0

Output for the Sample Input

5 1
9 1
7 1
8 2
98 2
8 2
8 3

题目大意：

有n只蚂蚁在一根木棍上（蚂蚁的编号从1~n），木棍是不是规则的，有的地方粗细不一致（详细请看图），每只蚂蚁方向朝左或者朝右，速度恒定1cm/s。在活动过程中，有可能会有两只蚂蚁相撞，如果他们相撞的地点位于木棍比较粗的地方，那么他们则不会改变方向，仍然向前行动。如果他们相撞的地点位于比较细的地方，则他们会立刻转向（改变方向的时间忽略不计）。现在要求，最后一只蚂蚁从木棍上掉下来的时刻是多少，还要输出是第几只蚂蚁。如果最后有几只蚂蚁同时掉落，则输出在木棍左边掉落的那只编号最小的蚂蚁。

解题思路：

看到这个题目，想到的就是刘汝佳的训练指南（白书）上的有一个关于蚂蚁的题目（忘了是哪页，反正应该就在前几页）。里面介绍了求蚂蚁运动的时间，即最后一只蚂蚁出来的时间是多少。详细请看白书。当求出时间之后，就可以根据时间来对蚂蚁的运动状态进行更新了，纯粹的模拟（但是其中有几个地方需要注意）看下面的代码吧。

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<string>
#include<stack>
#include<queue>
#include<vector>
#include<algorithm>
#include<iostream>
using namespace std;

struct point
{
    int loc;//蚂蚁的坐标
    int dir;//蚂蚁的方向
}p[50];
int n,len;
int num[50];
int t[50];//原本是写成time[50],我在AIZU上面交了几次，返回CE。后来才知道oj上面显示这个跟time.h头文件冲突（我又没写这个头文件.....有点不懂），之后改了过来
int main()
{
    while(scanf("%d%d",&n,&len)&&n&&len)//n代表蚂蚁的数目,len代表木棍的长度
    {
        for(int i=1;i<=n;i++)
        {
            getchar();//因为%c输入会吃掉回车符
            char a;
            int b;
            scanf("%c %d",&a,&b);
            p[i].loc=b;
            if(a=='R')
                p[i].dir=1;
            else
                p[i].dir=0;
            if(p[i].dir)//根据白书上的思路，先把时间求出来
                t[i]=len-p[i].loc;
            else
                t[i]=p[i].loc;
        }
        sort(t+1,t+1+n);//排序得到的t[n]，就是最后一个蚂蚁出来的时间了
        for(int i=1;i<=t[n];i++)
        {
            for(int j=1;j<=n;j++)//每一秒钟，更新一次蚂蚁的状态（坐标和方向）
            {
                if(p[j].dir)
                {
                    p[j].loc++;
                }
                else
                {
                    p[j].loc--;
                }
            }
            for(int j=1;j<n;j++)//这个处理要注意
            {
                for(int k=j+1;k<=n;k++)
                {
                    if(p[j].loc==p[k].loc)//判断如果有两只蚂蚁的位置一样，说明他们相撞了，那么就改变他们的方向
                    {
                        p[j].dir=!p[j].dir;
                        p[k].dir=!p[k].dir;
                    }
                }
            }
        }
        int cnt=0;//判断是否最后有多个蚂蚁同时出来
        for(int i=1;i<=n;i++)
        {
            if(p[i].loc==0||p[i].loc==len)//出来那么就代表他此时的位于木棍的左端或者右端（之前出来的蚂蚁此时坐标都是大于木棍的长度或者是小于零了）
            {
                num[cnt++]=i;//记录蚂蚁的编号
            }
        }
        if(cnt==1)
            printf("%d %d\n",t[n],num[0]);
        else
        {
            for(int i=0;i<cnt;i++)
            {
                if(!p[num[i]].dir)
                {
                    printf("%d %d\n",t[n],num[i]);
                    break;
                }
            }
        }
    }
    return 0;
}