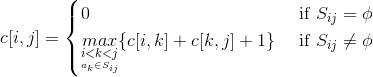《算法导论》笔记 第16章 16.1 活动选择问题
【笔记】
n个活动组成的集合S={a1,a2,...,an},每个活动ai有个开始时间si和结束时间fi,且0<=si<fi<OO。
如果区间[si,fi)和[sj,fj)互不重叠,称活动ai和aj是兼容的。
活动选择问题的最优子结构:
Sij={ak∈S : fi<=sk<fk<=sj}
Sij是S中活动的子集,其中每个活动都在a_i结束之后开始,且在a_j开始之前结束。
设活动按结束时间的单调递增顺序排序f0<=f1<=f2<=...<=fn<fn+1
断言,当i>=j时,Sij=∅。
最优解Aij:Aij=Aik∪{ak}∪Akj
整个问题的最优解也是S_{0,n+1}的一个解。
一个递归解:
将动态规划解转为贪心解:
对于任意非空子问题Sij,设am是Sij中具有最早结束时间的活动:fm=min{fk:ak∈Sij}
那么,
1) 活动am在Sij的某最大兼容活动子集中被使用。
2) 子问题Sim为空,所以选择am将使子问题Smj为唯一可能非空的子问题。
递归贪心算法
迭代贪心算法
A = {a1}
i = 1
for (int m=2;m<=n;m++) {
if (s[m]>=f[i]) {
A = A ∪ {a[m]}
i = m
}
}
【练习】
16.1-1 给出活动选择问题的动态规划算法。比较其运行时间与贪心算法的运行时间。
贪心时间O(n),DP时间O(n^2)。
16.1-2 假设不再总是选择第一个结束的活动,而选择最后一个开始、且与之前选入活动兼容的活动。说明如何成为贪心算法,并证明能得到最优解。
16.1-3 假设要对很多个教室对一组活动进行调度。我们希望使用尽可能少的教室来调度所有的活动。请给出一个有效的贪心算法,来确定哪一个活动应使用哪一个教室。
16.1-4 并不是所有贪心都正确- -。