8.6.5 仿射变形
简单变形也包括许多具体的变形方式,例如球面变形,透视变形,复杂拓扑变形等,其算法各有差别。在AS3中,运用Matrix类进行的简单变形都属于仿射变形(Affine Transformations)。
所谓仿射变形,其特征就是一切变形都不会破坏线条的线性。变形后水平和垂直方向上的长度比例可以发生变化。但直线永远不会变成曲线。坐标系内各点的变换都是均匀的,不存在局部扭曲和象限的塌缩。一对平行线,无论经过多少次仿射变形,都将保持平行,不会有交集。
既然属于简单变形,所以仿射变形的过程可以写为数学函数表达式。仿射变形主要是通过变量乘以变换矩阵实现的。考虑到位移难以用矩阵乘法获得,所以需要引入了一个位移矢量加权。其通用数学表达式为:
f(x)=Ax+b
其中,A是一个变换矩阵,b表示平移矢量。通过这个数学公式,可以计算诸如平移,旋转,拉伸等仿射变形。
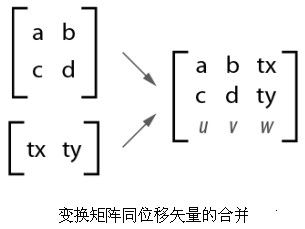
在计算机语言中,一般都会将位移矢量与变形矩阵合并在一个矩阵之中。这个矩阵为三行三列,左上角的两行两列是变形矩阵,第三列为平移矢量,并将余下的位置用数值补足。如图所示。
这种记法只是为了计算机程序构造的方便。虽然表面上是一个三行三列的矩阵,但在实际运算时,遵循的依然是f(x)=Ax+b的公式。
因为AS3中的Matrix类是处理仿射变形的,所以其功能有先天的限制。当处理复杂的变形时,必须另寻它途,在代码中自行创建变形函数去实现。如果不考虑这一点,在代码中尝试用Matrix类获得非仿射变形效果,则无异于南辕北辙,难以成功。