joj 1131: Intersection (判断直线与矩形是否有交点) .
Description
You are to write a program that has to decide whether a given line segment intersects a given rectangle.
An example:
line: start point: (4,9)
end point: (11,2)
rectangle: left-top: (1,5)
right-bottom: (7,1)
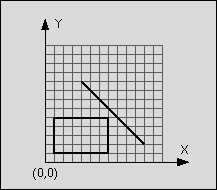
Figure 1: Line segment does not intersect rectangle
The line is said to intersect the rectangle if the line and the rectangle have at least one point in common. The rectangle consists of four straight lines and the area in between. Although all input values are integer numbers, valid intersection points do not have to lay on the integer grid.
Input
The input consists of n test cases. The first line of the input file contains the number n. Each following line contains one test case of the format:
xstart ystart xend yend xleft ytop xright ybottom
where (xstart, ystart) is the start and (xend, yend) the end point of the line and (xleft, ytop) the top left and (xright, ybottom) the bottom right corner of the rectangle. The eight numbers are separated by a blank. The terms top left and bottom right do not imply any ordering of coordinates.
Output
For each test case in the input file, the output file should contain a line consisting either of the letter "T" if the line segment intersects the rectangle or the letter "F" if the line segment does not intersect the rectangle.
Sample Input
1
4 9 11 2 1 5 7 1
Sample Output
F
巧妙的利用了这道题矩形四边与x轴 y轴垂直的条件,先判断线段所在直线是否穿过某一矩形对角线(1),若不穿过,则线段与矩形必不相交,若穿过再判断线段两个端点是否在矩形的一侧,因为有了条件(1)则不在一侧时必与矩形相交,否则不相交。
计算几何应避免除法,所以 直线方程应设为(y1-y2)*x+(x2-x1)*y+x1*y2-x2*y1=0.而不是kx-y+b=0的形式,因为设为点斜式需要考虑到斜率k不存在的情况,相比之下我们选用两点式。
#include <iostream>
using namespace std;
struct node
{
int x,y;
}m1,m2,s,e;
int main ()
{
int n;
cin>>n;
while (n--)
{
cin>>s.x>>s.y>>e.x>>e.y>>m1.x>>m1.y>>m2.x>>m2.y;
int a=s.y-e.y , b=e.x-s.x , c=e.y*s.x-e.x*s.y; //这样两点式就变成了a*x+b*y+c=0.
if(m1.x>m2.x){int x=m1.x ; m1.x=m2.x ; m2.x=x ;} //调换顺序
if(m1.y<m1.y){int y=m1.y ; m1.y=m2.y ; m2.y=y ;}
if( ((a*m1.x+b*m1.y+c)*(a*m2.x+b*m2.y+c))<=0 || ((a*m2.x+b*m1.y+c)*(a*m1.x+b*m2.y+c))<=0 ) //判断线段所在直线是否穿过矩形
{
if( (s.x<m1.x && e.x<m1.x)||(s.x>m2.x && e.x>m2.x)|| //进一步判断线段本身是否穿过矩形,
(s.y>m1.y && e.y>m1.y)||(s.y<m2.y && e.y<m2.y) ) //要想线段不穿过矩形,则线段只能在矩形的四个边的外边
cout<<"F"<<endl;
else cout<<"T"<<endl;
}
else cout<<"F"<<endl; //直线没穿过
}
return 0;
}