poj 2528 Mayor's posters(线段树区间更新+离散化)经典题目,较难。。。
1、http://poj.org/problem?id=2528
2、题目大意:
有一面墙,宽度是10000000,现在要在这面墙上贴海报,每张海报的高度都是墙的高度,但是宽度不同,现在给出各个海报的宽度,按照贴的顺序,后贴的会覆盖先贴的,求都贴完后,能看到几张海报,一张海报只要露着一部分就算是一张可以看到的
3、思路:
由于题目中wall有10000000bytes long,直接线段树无疑会MLE。所以要对其离散化,基本做法是:先对所有端点坐标进行排序,用相应序号代替端点坐标构造线段树进行计算。这样最大的序号也只是2*n。
离散化就是将n个数,都转换成较小的数,唯一不变的是这n个数的大小关系
例如 1 3 4 5 10000,就可以依次对应成0 1 2 3 4
这道题目不仅仅是保留这n个数的大小关系,还得保留他们之间的距离关系
例如这样一个样例
1 10
1 5
6 10
那么这个样例应该答案是2
1 5 6 10,离散化后是0 1 2 3,答案对
如果样例换成
1 10
1 4
6 10
1 4 6 10,离散化后还是0 1 2 3,这样做就不对了,因为没有考虑到4和6之间还有空
我们只要加一层循环就可以了,看一下如果后一个数字a[i]比前一个a[i-1]大的超过1,那么就在原有数组的基础上加上一个a[i-1]+1,那么1 4 6 10离散化后就是1 2 4 5 6 7 10
3、题目:
Mayor's posters
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 37297 | Accepted: 10844 |
Description
The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.
- Every candidate can place exactly one poster on the wall.
- All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
- The wall is divided into segments and the width of each segment is one byte.
- Each poster must completely cover a contiguous number of wall segments.
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.
Input
The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l
i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l
i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l
i, l
i+1 ,... , ri.
Output
For each input data set print the number of visible posters after all the posters are placed.
The picture below illustrates the case of the sample input.
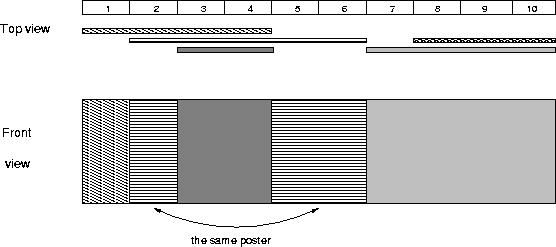
The picture below illustrates the case of the sample input.

Sample Input
1 5 1 4 2 6 8 10 3 4 7 10
Sample Output
4
Source
Alberta Collegiate Programming Contest 2003.10.18
4、AC代码:
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
#define N 10005
int s[N*4],e[N*4];
int a[N*4];
int col[N*16],visit[N*4],cnt;
int cmp(int a,int b)
{
return a<b;
}
int binarySearch(int key,int l,int r)
{
while(l<=r)
{
int m=(l+r)>>1;
if(key==a[m])
return m;
if(key<a[m])
r=m-1;
else
l=m+1;
}
return -1;
}
void pushDown(int rt)
{
if(col[rt]!=-1)
{
col[rt<<1]=col[rt<<1|1]=col[rt];
col[rt]=-1;
}
}
void update(int L,int R,int c,int l,int r,int rt)
{
if(L<=l && R>=r)
{
col[rt]=c;
return ;
}
pushDown(rt);
int m=(l+r)>>1;
if(L<=m)
update(L,R,c,l,m,rt<<1);
if(R>m)
update(L,R,c,m+1,r,rt<<1|1);
}
void query(int l,int r,int rt)
{
if(col[rt]!=-1)
{
if(visit[col[rt]]==0)
{
cnt++;
}
visit[col[rt]]=1;
return ;
}
if(l==r)
return ;
int m=(l+r)>>1;
query(l,m,rt<<1);
query(m+1,r,rt<<1|1);
}
int main()
{
int t,n;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
int j=0;
for(int i=1;i<=n;i++)
{
scanf("%d%d",&s[i],&e[i]);
a[j++]=s[i];
a[j++]=e[i];
}
sort(a,a+j,cmp);
int k=1;
for(int i=1;i<j;i++)
{
if(a[i]!=a[i-1])
a[k++]=a[i];
}
int kk=k;
for(int i=1;i<kk;i++)
{
if(a[i]!=a[i-1]+1)
a[k++]=a[i-1]+1;
}
sort(a,a+k,cmp);
memset(col,-1,sizeof(col));
for(int i=1;i<=n;i++)
{
int L=binarySearch(s[i],0,k-1);
int R=binarySearch(e[i],0,k-1);
update(L,R,i,0,k-1,1);
}
cnt=0;
memset(visit,0,sizeof(visit));
query(0,k-1,1);
printf("%d\n",cnt);
}
return 0;
}
/*
5
1 1
2 2
3 3
4 4
1 4
*/