Apriori导论

作者：金良（[email protected]） csdn博客：http://blog.csdn.net/u012176591

Apriori算法简介

Apriori算法是频繁模式和关联规则挖掘( Association Rule Mining )中最基础的算法，它用于从一个事务集中发现频繁项集并推出关联规则。

关联规则的目的在于在一个数据集中找出项之间的关系，也称之为购物篮分析 (market basket analysis)。例如，购买鞋的顾客，有10%的可能也会买袜子，60%的买面包的顾客，也会买牛奶。这其中最有名的例子就是"尿布和啤酒"的故事了。
关联规则的应用场合。在商业销售上，关联规则可用于交叉销售，以得到更大的收入；在保险业务方面，如果出现了不常见的索赔要求组合，则可能为欺诈，需要作进一步的调查。在医疗方面，可找出可能的治疗组合；在银行方面，对顾客进行分析，可以推荐感兴趣的服务等等。

相关术语

这里用上文的购物篮分析 (market basket analysis)的例子介绍Apriori算法的几个术语：

• 事务集：每单销售的商品组合，是大大小小的项集，可能有重复的项集。

• 项集(itemset)：袜子、面包和牛奶都可以成为项，一个或一个以上不重复的项的任意的无序组合都可以成为项集。比如{袜子，牛奶}、{袜子，牛奶，面包}、{面包}等。由于其不重复性，故{袜子，袜子}应该记作{袜子}；由于其无序性，故{袜子，牛奶}和{牛奶，袜子}是同一个项集。
• k-项集(k-itemsets)：有k个项的项集，比如1-项集有{袜子}、{牛奶}和{面包}，3-项集只有一个，即{袜子，牛奶，面包}。
• 频繁项集(frequent itemset)：项集在事务集中频繁出现的项集。怎么算是频繁出现呢？这里有个判断标准，也就是下面的最小支持度的概念。
• 支持度(Support)和最小支持度(minsup)：二者都是个比率。最小支持度是一个事先约定的数字，支持度达到这个数字的项集就是频繁项集。
• 置信度(Confidence)和最小置信度(minconf)：置信度，即对A推荐B的置信度，为事务数据库中包含A的事务中同时也包含B的百分比。
• 提升度(Lift)：以度量此规则是否可用。描述的是相对于不用规则，使用规则可以提高多少。有用的规则的提升度大于1。计算方式为
  
  
  
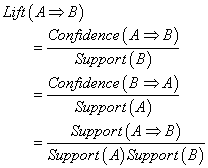
  举两个提升度的例子，对第一个，也就是说对买了A的人进行推荐B，购买概率是随机推荐B的1.32倍,所以需要对买了A的人推荐B；对第二个，对买了B和C的人推荐A，购买概率是不推荐时的0.74倍，所以没有必要对买了B和C的人推荐A。

Apriori算法描述

apriori算法的目的主要是查找所有频繁的项集，只要得到了频繁项集，就很容易找到满足最小置信度要求的项集。算法的关键在于它使用了一种分层的搜索算法,具体的说，先找到k-频繁项集，然后由k-频繁项集找(k+1)-频繁项集。为提高频繁项集逐层产生的效率，一种称作Apriori 性质的重要性质用于压缩搜索空间，它主要用了两个重要的性质

• 若X是频繁项集，则X的所有子集都是频繁项集。
• 若X是非频繁项集，则X的所有超集都是非频繁项集。

算法描述如下：

1. 将数据库中的事务的数据排序，首先将每条事务记录中多个元素排序，然后将事务整体排序。
2. 令k=1，扫描数据库，得到候选的1-项集并统计其出现次数，由此得到各个1-项集的支持度，然后根据最小支持度来提出掉非频繁的1-项集进而得到频繁的1-项集。
3. 令k=k+1.通过频繁（k-1）-项集产生k-项集候选集的方法（也称“连接步”）：
   如果两个（k-1）-项集，如果只有最后一个元素不同，其他都相同，那么这两个(k-1)-项集项集可以“连接”为一个k-项集。不能连接的就不用考虑了，不会频繁的。
4. 从候选集中剔除非频繁项集的方法（也称“剪枝步”）：
   对任一候选集，看其所有子项集(其实只需要对k-2个子项集进行判别即可)是否存在于频繁的(k-1)-项集中，如果不在，直接剔除；扫描数据库，算计数，最终确认得到的频繁的k-项集。
5. 如果得到的频繁的k-项集的数目<=1，则搜索频繁项集的过程结束；否则转到第3步。

Apriori算法伪代码可以描述如下：

下面对伪代码中出现的两个函数apriori-gen()和subset()进行说明：

伪代码中的subset函数，该函数以k阶候选项集 Ck和transaction t 为参数，输出为k阶候选项集被transaction t所包含的部分元素。

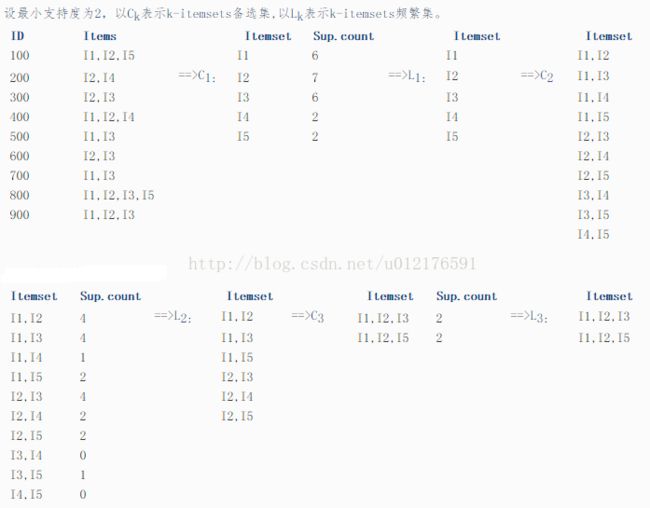
下面展示了用apriori算法查找频繁项集的一个例子。

Apriori算法查找频繁项集的实现代码

# -*- coding: UTF8 -*-
import sys
import copy
'''
事务集T = [['A','B','C','D'],['B','C','E'],\
['A','B','C','E'],['B','D','E'],['A','B','C','D']],按最小支持度0.3，找出其中的频繁项集
'''
 
# 采用字典的方式，记录元素的同时，也实现了计算元素个数
def single_count(T):
    C = {}
    for t in T:
        for i in t:
            if i in C.keys():
                C[i] += 1
            else:
                C[i] = 1
    return C
 


def is_equal_lists(lst1,lst2):
    if len(lst1) != len(lst2):
        return False
    else:
        n=len(lst1)
        for i in range(n):
            if lst1[i] != lst2[i]:
                return False
        return True
        
def candidate_gen(k_itemsets):
    C = []
    k = len(k_itemsets[0]) + 1  #当前F为K项集，则传入参数F为K-1项频繁集
    for f1 in k_itemsets:   #
        for f2 in k_itemsets:  
            if f1[k-2] < f2[k-2]:#比较两个K-1项集的最后一个元素，防止重复
                if is_equal_lists(f1[:k-2],f2[:k-2]):
                    c = copy.copy(f1)
                    c.append(f2[k-2])#连接步
                    flag = True
                    for i in range(0,k-2): #剪枝步，看子项集是否存在于频繁的(k-1)-项集中，如果不在，直接剔除
                        s = copy.copy(c) 
                        s.pop(i) 
                        if s not in k_itemsets:
                            flag = False 
                            break
                    if flag and c not in C:
                        C.append(c)
    return C


def compare_list(A,B):
    for a in A:
        if a not in B:
            return False
    return True
 
# 求出满足最小支持度的项目集合
def apriori(T, minsup):
    single_count_set = single_count(T) #
    keys = single_count_set.keys()  #得到1-项集的的列表
    keys.sort()  #排序
    C=keys #C为1-项候选集['A', 'B', 'C', 'D', 'E']
    n = len(T) #求出事物集的个数
    F = [[]]#F频繁项集的列表
    for f in C:
        if single_count_set[f]*1.0/n >= minsup:
            F[0].append([f])
    k = 1 # 此时获得1项目集          
    while F[k-1] != []:
        C=candidate_gen(F[k-1])
        F.append([]) #  这个很重要，每次先加入一个空集合
        for c in C:#依次拿出每个候选项集
            count = 0;
            for t in T: # 计算候选项集的支持度
                if compare_list(c,t): 
                    count += 1
            if count*1.0/n >= minsup:#判断候选项集是否是频繁项集
                F[k].append(c)
        k += 1
    U = []
    for f in F:#将二维列表变成一维列表
        for x in f:
            U.append(x)
    return U
 
def printlist(T):
    for i in range(len(T)):
        for j in range(len(T[i])):
            print T[i][j],
            
T = [['A','B','C','D'],['B','C','E'],['A','B','C','E'],['B','D','E'],['A','B','C','D']]
 
F = apriori(T, 0.3)
print '\n所有的频繁项集:\n'
print F
print '\n频繁项集的个数:\n'
print len(F)

运行效果：

哈希树(hash tree)及其在Apriori算法中的应用

再看apriori算法中的subset()函数，它用来查找k-阶候选集中被事务t 包含了的部分元素。其实该函数的效率是很低的，为了提高查找t所包含的候选项集的效率，就用到了哈希树。

hash tree(哈希树)，是由tree和hash table结合，旨在优化hash table冲突解决方案的一种数据结构。
在链式hash table中，若关键字发生冲突，则创建单个新节点链到冲突节点之后，并把关键字插入到新节点。
而在hash tree结构中，若关键字发生冲突，则创建一组新节点链到冲突节点之后，并把关键字hash后插入到某个新节点中。

• 哈希表可能效率较低，我们举个用哈希表存储数字的例子：
  对于数，当一个质数不够用的时候，可以加上第二个质数，用两个mod来确定该数据在库中的位置。那么这里需要简单的解释一下，对于一个质数x，它的mod有[ 0 .. x - 1 ] x种；所以对于两个质数x和y，能存储的无一重复的数据有 x *y 个，其实也就是开一个x*y的二维数组。但是当数据极其多时，用两个质数去mod显然也是有不够的时候，就还要再加一个。为了便于查找，选取最小的十个质数，也就是2，3，5，7，11，13，17，19，23，29来mod，就需要开辟能够存储6469693230个数字的空间，这太浪费存储资源了。这时就可以用到树。
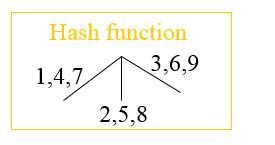
  下面是用哈希树存储0-5这六个整数的例子，可以看到，当查找某个数时，只要从根节点开始求余两次即可。例如查找整数3时，从根节点，先对3除2求余，得到余数1；由余数1进入右边的分支，然后对3除3求余得到余数0，进入左边分支到达叶节点3，查找完毕。
  
  当在上面的树上再插入数据8时，发现与原来的数据2发生了冲突，怎么办呢？这时需要对哈希树进行扩增，我们将原来2所在的叶节点转变成内节点，并令数据经过该内节点时对素数5求余来决定数据的分支。然后，我们将发生冲突的两个数2和8对素数5求余，并将二者分别作为叶节点挂在刚才新增的内节点下，就完成了哈希树的扩增。如下图所示。
  

前边提到的Apriori算法中，为了计算每个候选项集的支持度，需要对每个候选项集浏览一遍数据库中的transaction记录；而哈希树方法采用了完全不同的思路，它先将所有的k-阶候选集存储在哈希树的结构的叶节点上，然后对每个transaction记录找到其包含的所有k-阶候选集，所以这个过程只需要浏览一遍数据库。

下面先讲述构建哈希树的过程：

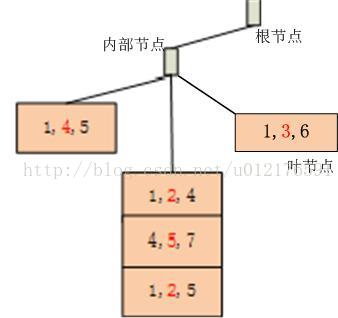
• 15个3-阶候选集，如下:
  {1 4 5}, {1 2 4}, {4 5 7}, {1 2 5}, {4 5 8}, {1 5 9}, {1 3 6}, {2 3 4}, {5 6 7}, {3 4 5}, {3 5 6}, {3 5 7}, {6 8 9}, {3 6 7}, {3 6 8}

• 叶子节点上最大的项集数是3
  当某个叶子上悬挂的项集数大于条件限制3(也就是项集数是4个)时，要进行分裂(split)操作。
• 哈希函数如下图所示：
  
  该哈希函数的解释：当数字是1、4或7时走向左分支，数字是2、5或8时走向中间分支，数字是3、6或9时走向右分支。

插入第一个项集时，哈希树只有一个根节点，深度level为1，所以用项集的第1项做hash，映射到根节点的左子树，于是得到：

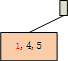
插入第二项集时，深度不变，仍然用第1项做hash,映射到同一个叶节点：

第三项插入时同理：

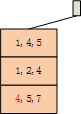
当插入第四项时，也是影射到同一个叶节点，但是该叶节点上的项集的数目大于3个，需要进行分裂操作，该叶节点变成了内部节点，要把这4个项集以第2项做hash，映射到新的叶节点。为什么要用第二项做哈希而不是原来的第一项呢？因为分裂操作增加了一个内部节点实现了哈希树扩增，我们插入数据的节点的深度level由1变成了2。

需要说明的是，只要插入的项集、叶子上的最大项集数和哈希函数固定，最后生成的哈希树的结构域项集的插入顺序无关。

在上述性质下，我们继续上面的哈希树构建工作，我们暂时跳过第4、5个项集，直接插入第六个项集{1,3,6}，现在我们描述一下插入的过程：从根节点开始，先对第一项取哈希值得1，进入根节点的左分支，根节点的左分支上的节点是内部节点，所以我们对第二项取哈希得6，所以进入该内部节点的右分支，由于右分支上没有叶节点，所以新建一个叶节点，将项集{1,3,6}存储在这个新的叶节点上。如下图所示：

最终生成的哈希树结构如下，可以看到15个3-阶候选集存储在哈希树的叶子上：

给出一个transaction t {1,2,3,4,5}，按照上面的哈希函数Hash Function产生所有的3-阶子项集的过程可以用一个哈希树表示如下：

如果3-阶候选项集的哈希树已经构造完毕的前提下，给定一个transaction t{1,2,3,4,5}，查找该transaction包含了的3-阶候选项集的过程如下图所示：

AprioriTid算法

Apriori算法通过减少候选集的数量来获得良好的性能。然而，在频繁项集(frequent itemsets)很多或者最小支持度(minsup)很低的情况下，算法必须生成数量庞大的候选项集并且需要反复扫描数据库来检查数量庞大的候选项集，代价仍然很高。

为了解决反复扫描数据库的带来的代价高昂的问题，一种Apriori算法的变体AprioriTid算法被提出，它在第一次遍历数据库后就不再对数据库进行操作。

伪代码如下：

AprioriTid虽然有计算的额外开销，但是它的优点在于当k较大时存储的空间较小。因此，在算法的初始阶段，由于k较小，Apriori具有优势，在算法的后期，由于k可能很大，这时用AprioriTid比较好。由于Apriori和AprioriTid使用了相同的候选项集生成过程，因此对相同的项集进行计数，这样就可以将这两种算法结合使用。AprioriHybrid在最初的遍历中使用Apriori，当它预计适合存储在内存中时则使用AprioriTid算法。

由频繁项集生成关联规则

上边的内容讲述了如何由事务记录transaction生成频繁项集，下面介绍如何由频繁项集生成关联规则，或者说推荐规则，比如餐馆里根据顾客已经点的菜单向顾客推荐别的菜。可以看出这是个在频繁项集内求后验概率的问题。

• 直接算法：枚举每个频繁项集f的所有非空子集a，如果,即生成一条规则。规则推理的方法也可以这样解释：
  
  
• 第二种方法利用了层次的概念，利用了如下性质：
  
  推理如下：
  
  

下面的关联规则生成算法采用了利用了上面的性质，伪代码(文章最后附有LaTeX代码)如下：

参考文献

• 关联规则算法Apriori的学习与实现
  http://blog.sina.com.cn/s/blog_591a31d20100rqw4.html  
  规则的使用方法
• 大话数据挖掘3：APRIORI算法
  http://blog.sina.com.cn/s/blog_6255c70101019ks3.html 
  开头的术语定义和末尾的算法描述
• 数据挖掘十大经典算法之一--APRIORI
  http://blog.sina.com.cn/s/blog_6714456f01011sfx.html 
• 数据挖掘10大算法.XinDong Wu,Vipin Kumar
• PerformanceScalability.ppt，一份介绍hash tree在Apriori算法中的应用的PPT： 
  http://www.cs.kent.edu/~jin/DM07/PerformanceScalability.ppt
• lecture4.ppt，一份介绍Apriori算法及hash tree的PPT：
  http://www.dabi.temple.edu/~vucetic/cis526fall2004/lecture4.ppt 
• 进一步学习的网站有源码或数据集：
  FIMI workshop——Not only Apriori and FIM——FP-tree, ECLAT, Closed, Maximal
  http://fimi.cs.helsinki.fi/
  Christian Borgelt’s website
  http://www.borgelt.net/software.html
  Ferenc Bodon’s website
  http://www.cs.bme.hu/~bodon/en/apriori/
  

附带代码：

• sql语句源码
  

      \noindent{\bf INSERT INTO} $C_k$\\
      {\bf SELECT } $p.fitItemset_1,p.fitItemset_2,...,p.fitItemset_{k-1},q.fitItemset_{k-1}$\\
      {\bf FROM } $F_{k-1}p,F_{k-1}q$\\
      {\bf WHERE } $p.fitItemset_1=q.fitItemset_1,...,p.fitItemset_{k-2}=q.fitItemset_{k-2}$\\
      \indent $p.fitItemset_{k-1}<q.fitItemset_{k-1}$

  
  
• Apriori算法伪代码源码
  

  \documentclass[11pt]{ctexart}
  \usepackage[top=2cm, bottom=2cm, left=2cm, right=2cm]{geometry}
  \usepackage{algorithm}
  \usepackage{algorithmicx}
  \usepackage{algpseudocode}
  \usepackage{amsmath}
  
  \floatname{algorithm}{}
  \renewcommand{\algorithmicrequire}{\textbf{Input:}}
  \renewcommand{\algorithmicensure}{\textbf{Output:}}
  \newcommand{\myoutput}{\textbf{output }}
  \newcommand{\myadd}{\textbf{add }}
  \newcommand{\mycall}{\textbf{call }}
  \newcommand{\mydelete}{\textbf{delete }}
  \begin{document}
  \begin{algorithm}[h]
    \caption{Apriori algorithm}
    \begin{algorithmic}[1]
    \Require $F_1$:一阶频繁集;$\mathcal{D}$:数据库,包含所有transaction
    \Ensure  $Answer$:各阶频繁项集
    \State \{large 1-itemsets\};
    \For {$k=2;L_{k-1}\neq \phi;k++$}
          \State $//$generate $k$-candidates from $F_{k-1}$;
          \State $C_k=$apriori-gen$(F_{k-1})$;
          \ForAll {transactions $t\in \mathcal{D}$}
              \State $//$given $t$,find candidates contained in $t$ from $C_k$
              \State $C_t=$subset$(C_k,t)$;
              \ForAll {candidates $c \in C_t$}
                  \State $c.count$++
              \EndFor
          \EndFor
          \State $F_k=\{c\in C_k|c.count\geq minsup\}$
    \EndFor
    \State $Answer=\cup_k\{F_k\}$
    \end{algorithmic}
  \end{algorithm}
  \end{document}

  
  
  
• 关联规则生成算法源码
  

  \begin{algorithm}[h]
    \caption{Association Rule Generating algorithm}
    \begin{algorithmic}[1]
    \State $H_1=\phi$
      \ForAll{frequent k-itemset $f_k(k\geq 2)$} 
          \State $A=$ (k-1)-itemsets $ a_{k-1} \mathrm{~such~that~} a_{k-1} \subset f_k$
          \ForAll{$a_{k-1}\in A$}
              \State $conf = support(f_k)/support(a_{k-1})$
              \If {$conf \geq minconf$}
                  \State \myoutput the rule $a_{k-1}\Rightarrow(f_k-a_{k-1})$ 
                  \State \myadd $(f_k-a_{k-1})$ to $H_1$;
              \EndIf
          \EndFor
          \State \mycall AP-GENRULES($f_k,H_1$)
      \EndFor
      \Function{ap-genrules}{$f_k:$ frequent k-itemset,$H_m:$ set of m-itemset consequences}
      \If {$k > m+1$} 
          \State $H_{m+1}=$ apriori-gen($H_m$);
          \ForAll {$h_{m+1}\in H_{m+1}$}
              \State $conf=support(f_k)/support(f_k-h_{m+1})$;
              \If{$conf \geq minconf$}
                  \State \myoutput the rule $f_k-h_{m+1}\Rightarrow h_{m+1}$
              \Else
                  \State \mydelete $h_{m+1}$ from $H_{m+1}$ 
              \EndIf
          \EndFor
          \State \mycall AP-GENRULES$(f_k,H_{m+1})$;
      \EndIf 
      \EndFunction
    \end{algorithmic}
  \end{algorithm}
  

• AprioriTid算法伪代码源码
  

  \begin{algorithm}[h]
    \caption{AprioriTid algorithm}
    \begin{algorithmic}[1]
    \State $F_1=\{ $ frequent~1-itemsets $ \}$;
    \State $//~\overline{C}_k$中每个元素都具有$<TID,\{ID\}>$的形式，其中$TID$是事务的标识符，$\{ID\}$(标记为$C_t$)是事务$TID$中的一个潜在频繁$k$-项集的标识符，它的一个元素对应于一个事务$t$, 即$<t.TID,\{c\in C_k|c$ 在$t$中$\}>$
    \State $\overline{C}_1=\mathrm{~database~} D $;
    \For {$k=2;F_{k-1}\neq \phi;k++$}
          \State $//~$由$k-1$-阶频繁项集$F_{k-1}$生成$k$-阶候选集$C_k$
          \State $C_k=$apriori-gen($F_{k-1}$);
          \State $\overline{C}_k=\phi$;
          \ForAll {entry $t \in \overline{C}_{k-1}$}
              \State $//~$$C_t$和$t.set-of-itemsets$就是上面的事务$t$的$\{ID\}$所代表的候选频繁项集，只是阶数不同.对每个候选项$c\in C_k$，$(c-c[k])$和$(c-c[k-1])$是生成$c$的两个项集,当生成$c\in C_k$的两个项集都是事务$t$所包含的项集时，则$c\in C_k$也是事务$t$所包含的潜在的$k$-阶频繁项集
              \State $C_t=\{c\in C_k|(c-c[k])\in $ t.set-of-itemsets $ \wedge(c-c[k-1])\in $ t.set-of-itemsets $\}$;
              \If {$C_t\neq \phi$}
                  \State $\overline{C}_k=\overline{C}_k\cup\{<t.TID,C_t>\}$;
                  \State $//~$事务$t$包含的$k$-阶候选项集$c_k$的支持度增加$1$
                  \ForAll {candidate $c\in C_t$}
                      \State $c.count++$;
                  \EndFor
              \EndIf
          \EndFor
          \State $//~$根据支持度$count$的大小从候选集$C_k$找出$k$-阶频繁项集$F_k$
          \State $F_k=\{c\in C_k|c.count\geq minsup\}$;
    \EndFor
    \State $Answer=\cup_k\{F_k\}$;  
    \end{algorithmic}
  \end{algorithm}