POJ 1416(DFS)

Shredding Company

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4985		Accepted: 2860

Description

You have just been put in charge of developing a new shredder for the Shredding Company Although a "normal" shredder would just shred sheets of paper into little pieces so that the contents would become unreadable, this new shredder needs to have the following unusual basic characteristics. 

1.The shredder takes as input a target number and a sheet of paper with a number written on it. 

2.It shreds (or cuts) the sheet into pieces each of which has one or more digits on it. 

3.The sum of the numbers written on each piece is the closest possible number to the target number, without going over it. 

For example, suppose that the target number is 50, and the sheet of paper has the number 12346. The shredder would cut the sheet into four pieces, where one piece has 1, another has 2, the third has 34, and the fourth has 6. This is because their sum 43 (= 1 + 2 + 34 + 6) is closest to the target number 50 of all possible combinations without going over 50. For example, a combination where the pieces are 1, 23, 4, and 6 is not valid, because the sum of this combination 34 (= 1 + 23 + 4 + 6) is less than the above combination's 43. The combination of 12, 34, and 6 is not valid either, because the sum 52 (= 12 + 34 + 6) is greater than the target number of 50. 
 
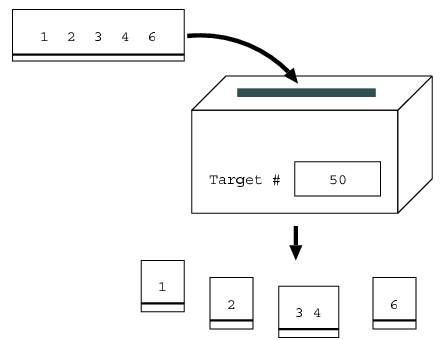
Figure 1. Shredding a sheet of paper having the number 12346 when the target number is 50

There are also three special rules : 

1.If the target number is the same as the number on the sheet of paper, then the paper is not cut. 

For example, if the target number is 100 and the number on the sheet of paper is also 100, then 

the paper is not cut. 

2.If it is not possible to make any combination whose sum is less than or equal to the target number, then error is printed on a display. For example, if the target number is 1 and the number on the sheet of paper is 123, it is not possible to make any valid combination, as the combination with the smallest possible sum is 1, 2, 3. The sum for this combination is 6, which is greater than the target number, and thus error is printed. 

3.If there is more than one possible combination where the sum is closest to the target number without going over it, then rejected is printed on a display. For example, if the target number is 15, and the number on the sheet of paper is 111, then there are two possible combinations with the highest possible sum of 12: (a) 1 and 11 and (b) 11 and 1; thus rejected is printed. In order to develop such a shredder, you have decided to first make a simple program that would simulate the above characteristics and rules. Given two numbers, where the first is the target number and the second is the number on the sheet of paper to be shredded, you need to figure out how the shredder should "cut up" the second number. 

Input

The input consists of several test cases, each on one line, as follows : 

tl num1 
t2 num2 
... 
tn numn 
0 0 

Each test case consists of the following two positive integers, which are separated by one space : (1) the first integer (ti above) is the target number, (2) the second integer (numi above) is the number that is on the paper to be shredded. 

Neither integers may have a 0 as the first digit, e.g., 123 is allowed but 0123 is not. You may assume that both integers are at most 6 digits in length. A line consisting of two zeros signals the end of the input. 

Output

For each test case in the input, the corresponding output takes one of the following three types : 

sum part1 part2 ... 
rejected 
error 

In the first type, partj and sum have the following meaning : 

1.Each partj is a number on one piece of shredded paper. The order of partj corresponds to the order of the original digits on the sheet of paper. 

2.sum is the sum of the numbers after being shredded, i.e., sum = part1 + part2 +... 

Each number should be separated by one space. 
The message error is printed if it is not possible to make any combination, and rejected if there is 
more than one possible combination. 
No extra characters including spaces are allowed at the beginning of each line, nor at the end of each line. 

Sample Input

50 12346
376 144139
927438 927438
18 3312
9 3142
25 1299
111 33333
103 862150
6 1104
0 0

Sample Output

43 1 2 34 6
283 144 139
927438 927438
18 3 3 12
error
21 1 2 9 9
rejected
103 86 2 15 0
rejected

Source

Japan 2002 Kanazawa

题意：

公司现在要发明一种新的碎纸机，要求新的碎纸机能够把纸条上的数字切成最接近而不超过target值。比如，target的值是50，而纸条上的数字是12346，应该把数字切成四部分，分别是1、2、34、6。因为这样所得到的和43 (= 1 + 2 + 34 + 6) 是所有可能中最接近而不超过50的。（比如1, 23, 4, 和6 就不可以,因为它们的和不如43接近50，而12, 34, 6也不可以，因为它们的和超过50了。碎纸还有以下三个要求：

1、如果target的值等于纸条上的值，则不能切。
2、如果没有办法把纸条上的数字切成小于target，则输出error。如target是1而纸条上的数字是123，则无论你如何切得到的和都比1大。
3、如果有超过一种以上的切法得到最佳值，则输出rejected。如target为15，纸条上的数字是111，则有以下两种切法11、1或者1、11.
你的任务是编写程序对数字进行划分以达到最佳值。

题解：

直接dfs就可以啦，只不过题意太长，容易把人吓到，dfs分解数字所有的可能性，找出符合题意的就可以了，这里如何判断会有多个最优解呢？使用数组保存最优解的次数即可，路径我是用string值传递，感觉还不错。可以降低编写难度，不用递归输出了

#include<cstdio>  
#include<cstring>  
#include<cstdlib>  
#include<cmath>  
#include<iostream>  
#include<algorithm>  
#include<vector>  
#include<map>  
#include<set>  
#include<queue>  
#include<string>  
#include<bitset>  
#include<utility>  
#include<functional>  
#include<iomanip>  
#include<sstream>  
#include<ctime>  
using namespace std;
#define N int(1e6)
int ans;
int vis[N];
string despath;

void dfs(int tgt, int k,string path,int dep,int sum)
{
	if (dep == 0)
	{
		if (sum <= tgt&&ans<=sum)
		{
			despath = path;
			ans = max(ans, sum);
			vis[ans]++;
		}
		return;
	}
	for (int i = 1; i <= dep; i++)
	{
		int num = 0;
		string tmp = path;
		int div = 1;
		int w = k;
		for (int j = 0; j < i; j++)
		{

			num += (w% 10)*div;
			tmp += (w % 10 + '0');
			div *= 10;
			w /= 10;
		}
		tmp += " ";
		dfs(tgt, k / div,tmp,dep-i,sum+num);
	}
}


void print()
{
	printf("%d", ans);
	for (int i = despath.size() - 1; i >= 0; i--)
		putchar(despath[i]);
	puts("");
}

int main()
{
#ifdef CDZSC  
	freopen("i.txt", "r", stdin);
	//freopen("o.txt","w",stdout);  
	int _time_jc = clock();
#endif  
	int n,k;
	while (~scanf("%d%d", &n, &k))
	{
		despath.clear();
		ans = -1;
		memset(vis, 0, sizeof(vis));
		if (n == 0 && k == 0)break;
		if (n == k)
		{
			printf("%d %d\n", n, k);
		}
		else
		{
			int tmp = k,rud=0;
			while (tmp > 0){tmp /= 10; rud++;}
			string path; path.clear();
			dfs(n, k,path,rud,0);
			if (ans == -1)
			{
				puts("error");
			}
			else
			{
				if (vis[ans] == 1)
				{
					print();
				}
				else
				{
					puts("rejected");
				}
			}
		}
	}
	return 0;
}