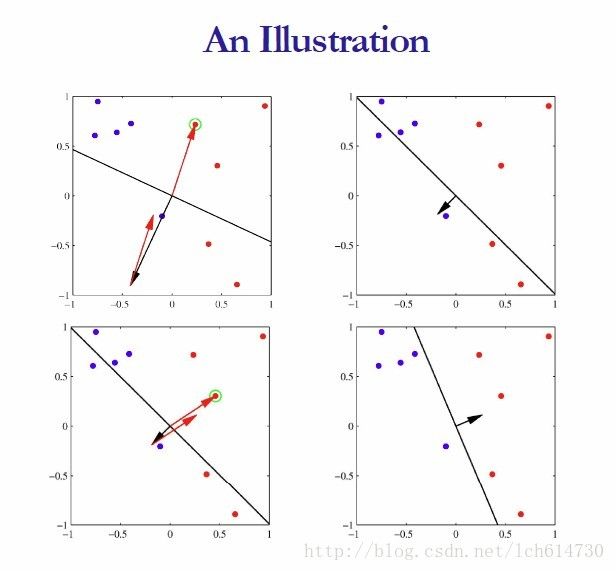
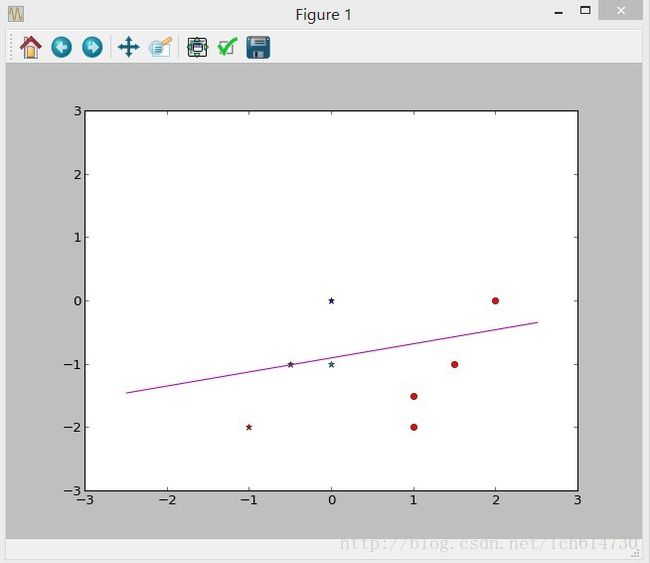
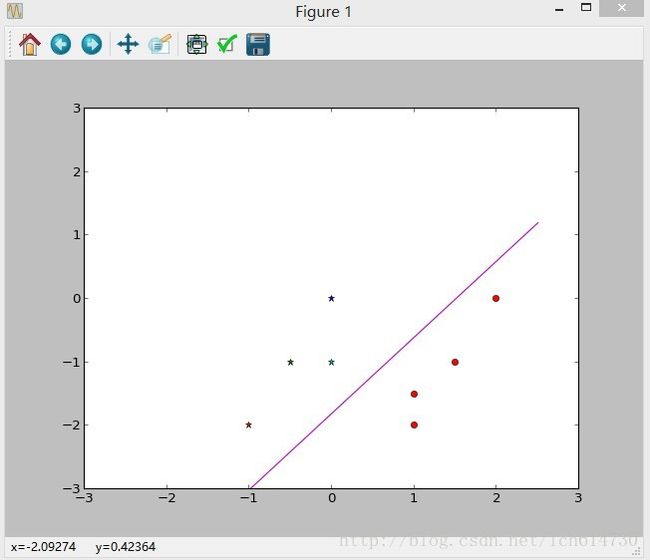
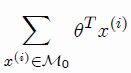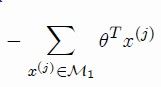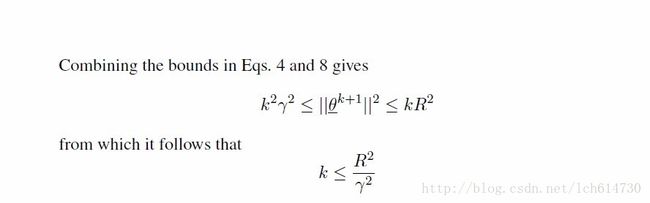Digression:The perceptron learning algorithm(感知机学习算法)
Digression:The perceptron learning algorithm
离散:(感知机学习算法)
本章主要讲解感知机算法:
1. 感知机算法的假设函数
2. 感知机算法的损失函数含说明,收敛性的证明
3. 感知机学习算法的参数更新 SGD
4. 感知机python代码演示
--------------------------------------------------------------------------------------------------------------------------------------------------
前言:
最近在研究机器学习理论的时候发现了一本好书,是李航博士的《统计学习方法》,书写得深入浅出,直白易懂,虽然不厚,但把统计学习各个方面都照顾到了,非常适合我这种机器学习方面的入门者,于是产生了一种写写读书笔记的想法,至少在日后看起来,也算是自己在追求大道上的一点回忆。
先给出书的豆瓣链接:《统计学习方法》,书真的很好,再次推荐!
先给出书的豆瓣链接:《统计学习方法》,书真的很好,再次推荐!
本文主要参考了博客园的作者文章:http://www.cnblogs.com/OldPanda/archive/2013/04/12/3017100.html
1. 感知机算法的假设函数(模型)
我们先来定义一下什么是感知机?所谓感知机,就是二类分类的线性分类模型,其输入为样本的特征向量,输出为样本的类别,取 +1 和 -1 二值(自己可以随便定义这个离散值,只要能分开两类的boolean就行的),即通过某样本的特征,就可以准确判断该样本属于哪一类。顾名思义,感知机能够解决的问题首先要求特征空间是线性可分的,再者是二类分类,即将样本分为{+1, -1}两类。从比较学术的层面来说,由输入空间到输出空间的函数:
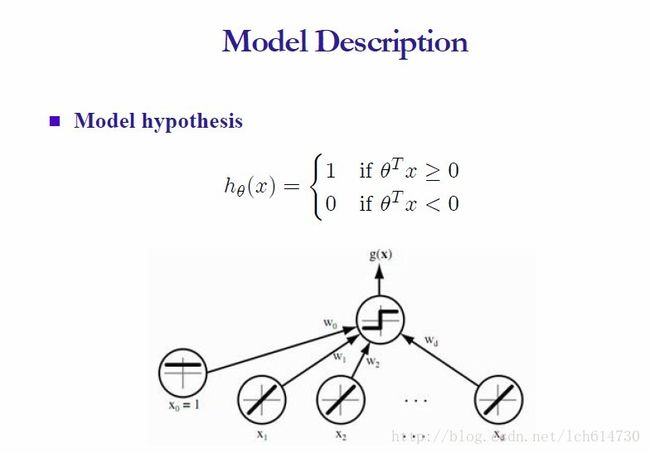
感知机的假设函数其实就是类别标签的值,一般有很多中表达方式:
(1) 最常用的表达方式:{-1,1}的形式
(2) 今天我们讲解的模型为: {1,0}的形式
从上面的公式我们已经知道,类别标签使我们自己定义的离散值,例如{0,1}或者{-1,1}都可以! 而我们的假设函数就是根据类别标签来设置的,如何设置呢?为了表示2个类别,最终理想的分类函数为 W
T
X = 0,W,X都是向量
我们就用 WTX(i) >= 0 表示标签 1,用 WTX(i) < 0表示标签 0(或 -1)
2. 感知机算法的损失函数含说明,收敛性的证明
为什么损失函数会使上面的 Jp(theta)?
答:
我们也知道调节过后最终最理想的情况就是:类别标签值 和类别所对应的假设函数值 应该相等!!即,此时的真实值和估计值相等 Error ==0,换言之,这个时候 Jp(theta)== 0。
但是,当我们的 参数均处于初始值状态下时,有很多点是错分的,就有两种情况:
(1)本来属于 0 类(y=0)的点错分到 1 类去了
错分到1类之后,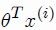 >=0,即 h(theta)= 1,y = 0所有以上求和就是所有0类错分到1类的点 函数权值之和必>=0
>=0,即 h(theta)= 1,y = 0所有以上求和就是所有0类错分到1类的点 函数权值之和必>=0
(2)本来属于 1 类(y = 1)的点错分到 0 类去了
错分到0类之后,
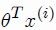 <
0,即 h(theta)= 0,y = 1所有以上求和就是所有1类错分到0类的点
函数权值之和必<0,在前面加上 -负号成为正数了。
<
0,即 h(theta)= 0,y = 1所有以上求和就是所有1类错分到0类的点
函数权值之和必<0,在前面加上 -负号成为正数了。
总 结:
将两类联合到一起我们可以写成:
我们只看上图的红色线条圈出的 M
0
情况,就是当0类 错分到1类 时各个值的情况如下:
---------------------------------------------------------------------------------------
y(i) = 0 (因为这是事先我们给好的标签,就是第0类!!)
---------------------------------------------------------------------------------------
h( x(i) ) = 1 (因为这个时候被错分了,所以 thetaT *X(i) >= 0)
---------------------------------------------------------------------------------------
{ (1 - yi ) * h(xi) - yi *(1 - h(xi) ) } * thetaT xi = thetaT xi >= 0
---------------------------------------------------------------------------------------
而理想的情况(没有错分的话):h(xi)- yi == 0 (必然是这样)
同理,M1的情况也好分析,就是前面取个负号-, - thetaT xi > 0
因此我们得出的结论就是:
只要有错分了的情况下 Jcost_functions >= 0,
全分对的情况(当然这是最理想的情况)Jcost_functions == 0 或者是无限接近于 0
所以,只需要是Jcost_function无限接近于0 或者等于0 啊,这就是最小化优化问题啦,我们以前用过梯度下降法,坐标轮换法,等等!
------------------------------------------------------------------------------------------------------------------
收敛性证明
详情请参考:
哥伦比亚大学有这样的一篇叫《 Convergence Proof for the Perceptron Algorithm
》的笔记
3. 感知机学习算法的参数更新 SGD
4. 感知机python代码演示
'''
Author :Chao Liu
Data:2013/12/9
Algorithm: perceptron
'''
import numpy
import matplotlib.pyplot as plt
'''
decision function
'''
def h_function(W,x):
value = numpy.dot(W,x)
if value >= 0.0:
return 1
else:
return 0
'''
cost function
'''
def Jcost_function(W,X,Y):
sum = 0.0
for i in range(len(Y)):
sum += (h_function(W,X[i]) - Y[i]) * numpy.dot(W,X[i])
return sum
'''
SGD method
'''
def SGD(W,X,Y,learning_rate,limit,max_iter):
cnt = 0
Jcost_pre = Jcost_function(W,X,Y)
print 'init cost = ',Jcost_function(W,X,Y)
x = [-2.5,2.5]
y = [0.0]*2
while cnt < max_iter:
for i in range(len(Y)):
if (Y[i] == 1 and h_function(W,X[i]) == 0):
W = W + numpy.dot(learning_rate,X[i])
print 'W = ',W
print 'cost = ',Jcost_function(W,X,Y)
elif (Y[i] == 0 and h_function(W,X[i]) == 1):
W = W - numpy.dot(learning_rate,X[i])
print 'W = ',W
print 'cost = ',Jcost_function(W,X,Y)
else:
print 'this point ',X[i],' do not need to update!'
if (Jcost_pre - Jcost_function(W,X,Y)) < limit:
print 'this Algotithm is convergence!!'
break;
Jcost_pre = Jcost_function(W,X,Y)
cnt += 1
for i in range(len(Y)):
if Y[i] == 1:
plt.plot(X[i][0],X[i][1],'*')
else:
plt.plot(X[i][0],X[i][1],'or')
plt.xlim(-3,3)
plt.ylim(-3,3)
for i in range(len(x)):
y[i] = -((W[0]*x[i]+W[2])/W[1])
plt.plot(x,y)
plt.show()
if __name__ == '__main__':
# W = [theta1,theta2,theta0]
W = [1.0,1.0,1.0]
X = [(0,0,1),(-0.5,-1,1),(-1,-2,1),(0,-1,1),(1,-1.5,1),(2,0,1),(1.5,-1,1),(1,-2,1)]
Y = [1,1,1,1,0,0,0,0]
SGD(W,X,Y,0.1,0.001,10)
Author :Chao Liu
Data:2013/12/9
Algorithm: perceptron
'''
import numpy
import matplotlib.pyplot as plt
'''
decision function
'''
def h_function(W,x):
value = numpy.dot(W,x)
if value >= 0.0:
return 1
else:
return 0
'''
cost function
'''
def Jcost_function(W,X,Y):
sum = 0.0
for i in range(len(Y)):
sum += (h_function(W,X[i]) - Y[i]) * numpy.dot(W,X[i])
return sum
'''
SGD method
'''
def SGD(W,X,Y,learning_rate,limit,max_iter):
cnt = 0
Jcost_pre = Jcost_function(W,X,Y)
print 'init cost = ',Jcost_function(W,X,Y)
x = [-2.5,2.5]
y = [0.0]*2
while cnt < max_iter:
for i in range(len(Y)):
if (Y[i] == 1 and h_function(W,X[i]) == 0):
W = W + numpy.dot(learning_rate,X[i])
print 'W = ',W
print 'cost = ',Jcost_function(W,X,Y)
elif (Y[i] == 0 and h_function(W,X[i]) == 1):
W = W - numpy.dot(learning_rate,X[i])
print 'W = ',W
print 'cost = ',Jcost_function(W,X,Y)
else:
print 'this point ',X[i],' do not need to update!'
if (Jcost_pre - Jcost_function(W,X,Y)) < limit:
print 'this Algotithm is convergence!!'
break;
Jcost_pre = Jcost_function(W,X,Y)
cnt += 1
for i in range(len(Y)):
if Y[i] == 1:
plt.plot(X[i][0],X[i][1],'*')
else:
plt.plot(X[i][0],X[i][1],'or')
plt.xlim(-3,3)
plt.ylim(-3,3)
for i in range(len(x)):
y[i] = -((W[0]*x[i]+W[2])/W[1])
plt.plot(x,y)
plt.show()
if __name__ == '__main__':
# W = [theta1,theta2,theta0]
W = [1.0,1.0,1.0]
X = [(0,0,1),(-0.5,-1,1),(-1,-2,1),(0,-1,1),(1,-1.5,1),(2,0,1),(1.5,-1,1),(1,-2,1)]
Y = [1,1,1,1,0,0,0,0]
SGD(W,X,Y,0.1,0.001,10)