《leetCode》：Search in Rotated Sorted Array

题目

Suppose a sorted array is rotated at some pivot unknown to you beforehand.

(i.e., 0 1 2 4 5 6 7 might become 4 5 6 7 0 1 2).

You are given a target value to search. If found in the array return its index, otherwise return -1.

You may assume no duplicate exists in the array.

题目大意：就是在一个由已排序的数组经过旋转而得到的数组中寻找目标target出现的下标。

思路一

最简单的思路就是：直接遍历一次数组，在数组中找出与target相等的下标即可；

实现代码如下：

//题目大意：找出target是有数组num旋转得到时的旋转轴
//思路：遍历一次数组即可 
int search(int* nums, int numsSize, int target) {
    if(nums==NULL||numsSize<1){
        return -1;
    } 
    bool flag=false;//标志是否匹配
    int i=0; 
    for(;i<numsSize;i++){//先找到最高位在数组中的位置 
        if(nums[i]==target){
            flag=true;
            break;
        } 
    }
    if(!flag){//没有找到
        return -1;
    }
    return i;
}

AC结果如下：

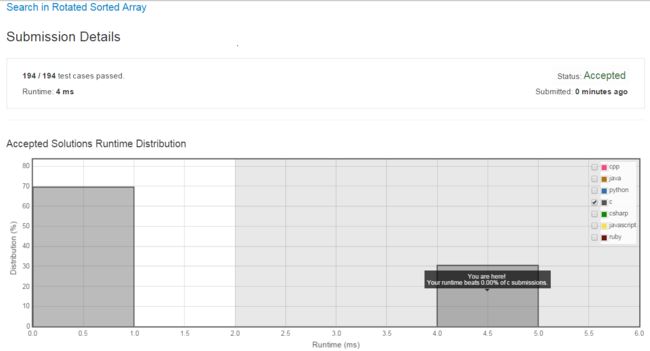
看到《leetCode》上面的这个题的难度是hard，原以为这样直接做会报时间超时，不能AC，后来提交居然AC了，真奇怪。

上面虽然AC了，但是自己知道此题目的考点并不是这样简单的遍历；而且也完全没有利用数组是由已排序的数组经过旋转得到的这个特点，而且从上面的AC结果可以看出，通过直接遍历一次的效率是不高的。因此需要改进

思路二：利用二分查找法

由于数组是由一个排序数组经过旋转得到的，因此数组会有如下的三种情况

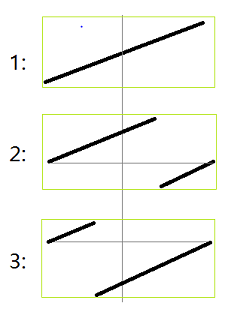
实现代码如下：代码可能比较长，但是。逻辑比较简单

/*
利用二分搜索来寻找目标 
*/
int binarysearch(int *nums,int begin,int end,int target){
    if(nums==NULL||(begin>end)){
        return -1;
    } 
    int mid=begin+(end-begin)/2;
    //将数组的begin/end/mid都与target进行比较 
    if(nums[mid]==target){
        return mid;
    }
    if(nums[end]==target){
        return end;
    }
    if(nums[begin]==target){
        return begin;
    }
    //第一种情况
    if(nums[end]>nums[begin]){
        if(target<nums[begin]||target>nums[end]){//target不在此范围中 
            return -1;
        }
        if(nums[mid]>target){
            end=mid-1;
            return binarysearch(nums,begin,end,target);
        }
        else{
            begin=mid+1;
            return binarysearch(nums,begin,end,target);
        }
    }
    //第二种情况
    else if(nums[mid]>nums[end]){
        if(nums[mid]>target&&target>nums[begin]){//在mid的左边 
            end=mid-1;
            begin=begin+1; 
            return binarysearch(nums,begin,end,target);
        }
        else {//target>nums[mid]在mid的右边 
            begin=mid+1;
            end=end-1;//由于是第二种情况，
            return binarysearch(nums,begin,end,target); 
        }

    }
    //第三种情况 
    else {
        if(nums[mid]<target&&target<nums[end]){//在mid右边 
            begin=mid+1;
            end=end-1;
            return binarysearch(nums,begin,end,target); 

        }
        else {//在mid的左边 
            end=mid-1;
            begin=begin+1;//由于最开始的地方就把两端和mid位置的值与target进行了比较 
            return  binarysearch(nums,begin,end,target); 
        }
    }

}
int search(int* nums, int numsSize, int target) {
    if(nums==NULL||numsSize<1){
        return -1;
    } 
    int begin=0;
    int end=numsSize-1;
    return binarysearch(nums,begin,end,target);
}

AC结果如下：

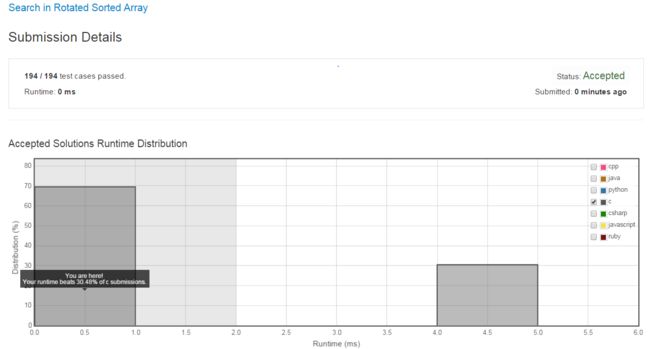
从结果可以看出，这种方法在效率上面有一定的改进。

精简思路二的代码

思路与思路二的一样，只是不是使用递归，而是使用while循环。

代码如下：

int search(int* nums, int numsSize, int target) {
    if(nums==NULL||numsSize<1){
        return -1;
    } 
    int begin=0;
    int end=numsSize-1;
    while(begin<=end){
        int mid=begin+(end-begin)/2;
        if(nums[mid]==target)  return mid;
        if(nums[begin]<nums[end]){//第一种情况
             if(nums[mid]>target)  end=mid-1;
             else begin=mid+1;
        }
        else if(nums[mid]>nums[end]){//第二种情况 
            if(nums[mid]>target&&nums[begin]<=target){//在mid左边,注意等号 
                end=mid-1; 
            }
            else{
                begin=mid+1;
            }
        } 
        else{//第三种情况 
            if(nums[mid]<target&&nums[end]>=target){//在mid的右边，注意等号 
                begin=mid+1; 
            }
            else{
                end=mid-1;
            }
        } 
    }
    return -1;
}

这种方法只是在代码有一定的精简，在效率上一样。

今天就到此为止了，跑步去了，吼吼