POJ 2284 That Nice Euler Circuit (欧拉定理)
Description
Little Joey invented a scrabble machine that he called Euler, after the great mathematician. In his primary school Joey heard about the nice story of how Euler started the study about graphs. The problem in that story was - let me remind you - to draw a graph on a paper without lifting your pen, and finally return to the original position. Euler proved that you could do this if and only if the (planar) graph you created has the following two properties: (1) The graph is connected; and (2) Every vertex in the graph has even degree.
Joey's Euler machine works exactly like this. The device consists of a pencil touching the paper, and a control center issuing a sequence of instructions. The paper can be viewed as the infinite two-dimensional plane; that means you do not need to worry about if the pencil will ever go off the boundary.
In the beginning, the Euler machine will issue an instruction of the form (X0, Y0) which moves the pencil to some starting position (X0, Y0). Each subsequent instruction is also of the form (X', Y'), which means to move the pencil from the previous position to the new position (X', Y'), thus draw a line segment on the paper. You can be sure that the new position is different from the previous position for each instruction. At last, the Euler machine will always issue an instruction that move the pencil back to the starting position (X0, Y0). In addition, the Euler machine will definitely not draw any lines that overlay other lines already drawn. However, the lines may intersect.
After all the instructions are issued, there will be a nice picture on Joey's paper. You see, since the pencil is never lifted from the paper, the picture can be viewed as an Euler circuit.
Your job is to count how many pieces (connected areas) are created on the paper by those lines drawn by Euler.
Joey's Euler machine works exactly like this. The device consists of a pencil touching the paper, and a control center issuing a sequence of instructions. The paper can be viewed as the infinite two-dimensional plane; that means you do not need to worry about if the pencil will ever go off the boundary.
In the beginning, the Euler machine will issue an instruction of the form (X0, Y0) which moves the pencil to some starting position (X0, Y0). Each subsequent instruction is also of the form (X', Y'), which means to move the pencil from the previous position to the new position (X', Y'), thus draw a line segment on the paper. You can be sure that the new position is different from the previous position for each instruction. At last, the Euler machine will always issue an instruction that move the pencil back to the starting position (X0, Y0). In addition, the Euler machine will definitely not draw any lines that overlay other lines already drawn. However, the lines may intersect.
After all the instructions are issued, there will be a nice picture on Joey's paper. You see, since the pencil is never lifted from the paper, the picture can be viewed as an Euler circuit.
Your job is to count how many pieces (connected areas) are created on the paper by those lines drawn by Euler.
Input
There are no more than 25 test cases. Ease case starts with a line containing an integer N >= 4, which is the number of instructions in the test case. The following N pairs of integers give the instructions and appear on a single line separated by single spaces. The first pair is the first instruction that gives the coordinates of the starting position. You may assume there are no more than 300 instructions in each test case, and all the integer coordinates are in the range (-300, 300). The input is terminated when N is 0.
Output
For each test case there will be one output line in the format
Case x: There are w pieces.,
where x is the serial number starting from 1.
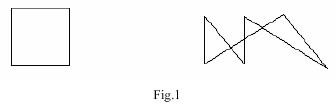
Note: The figures below illustrate the two sample input cases.
Case x: There are w pieces.,
where x is the serial number starting from 1.
Note: The figures below illustrate the two sample input cases.

Sample Input
5 0 0 0 1 1 1 1 0 0 0 7 1 1 1 5 2 1 2 5 5 1 3 5 1 1 0
Sample Output
Case 1: There are 2 pieces. Case 2: There are 5 pieces.
题意:平面上有n个端点的一笔画,第n个端点总是和第一个端点重合,因此图案是一条闭合曲线。组成一笔画的线段可以相交但是不会部分重叠,求这些线段将平面分成了几个部分(包括封闭区域和无限大区域)
欧拉定理:设平面图的顶点数,边数和面数分别为V,E,F 则V+F-E=2
这样只需求出顶点数和边数,就可以求出面数。该平面图的节点由原来的节点和新增的节点组成,由于可能出现三线共点需要删除重复的点
#include <iostream>
#include <algorithm>
#include <math.h>
using namespace std;
struct Point
{
double x,y;
Point(){}
Point(double x,double y):x(x),y(y){}
};
Point operator+(Point A,Point B)
{
return Point(A.x+B.x,A.y+B.y);
}
Point operator-(Point A,Point B)
{
return Point(A.x-B.x,A.y-B.y);
}
Point operator*(Point A,double p)
{
return Point(A.x*p,A.y*p);
}
Point operator/(Point A,double p)
{
return Point(A.x/p,A.y/p);
}
bool operator<(const Point&a,const Point&b)
{
return a.x<b.x||(a.x==b.x&&a.y<b.y);
}
double Cross(Point A,Point B)//求叉积
{
return A.x*B.y-A.y*B.x;
}
int dcmp(double x)//相等函数
{
double eps=1e-10;
if(fabs(x)<eps)return 0;
else return x<0?-1:1;
}
bool operator == (const Point& a, const Point& b)
{
return dcmp(a.x - b.x) == 0 && dcmp(a.y - b.y) == 0;
}
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2)//判断线段相交
{
double c1=Cross(a2-a1,b1-a1),c2=Cross(a2-a1,b2-a1);
double c3=Cross(b2-b1,a1-b1),c4=Cross(b2-b1,a2-b1);
return dcmp(c1)*dcmp(c2)<0&&dcmp(c3)*dcmp(c4)<0;
}
Point GetLineIntersection(Point P,Point v,Point Q,Point w)//求直线的交点
{
Point u=P-Q;
double t=Cross(w,u)/Cross(v,w);
return P+v*t;
}
double Dot(Point A,Point B)//点积
{
return A.x*B.x+A.y*B.y;
}
bool OnSegment(Point p,Point a1,Point a2)//判断一个点是否在一条线段上(不包含端点)
{
return dcmp(Cross(a1-p,a2-p))==0&&dcmp(Dot(a1-p,a2-p))<0;
}
int main()
{
int N,cases=1;
while(cin>>N&&N!=0)
{
Point P[310],V[310*310];
for(int i=0;i<N;i++)//输入坐标
{
cin>>P[i].x>>P[i].y;
V[i]=P[i];
}
N--;//重复了一个元素
int v=N,e=N;//顶点数,边数的初始化
for(int i=0;i<N;i++)
for(int j=i+1;j<N;j++)
if(SegmentProperIntersection(P[i],P[i+1],P[j],P[j+1]))//穷举法看两两线段是否相交
V[v++]=GetLineIntersection(P[i],P[i+1]-P[i],P[j],P[j+1]-P[j]);//保留因为线段相交产生的新节点
sort(V,V+v);
v=unique(V,V+v)-V;//unique去除相邻的重复的顶点,但实际上是将相同的数移到了数组的后面
for(int i=0;i<v;i++)
for(int j=0;j<N;j++)
if(OnSegment(V[i],P[j],P[j+1]))
e++;
cout<<"Case "<<cases++<<": There are "<<e+2-v<<" pieces."<<endl;
}
return 0;
}