zoj 1128 || poj 1151 Atlantis

求矩形并的面积。

 

传说中的离散化。

 

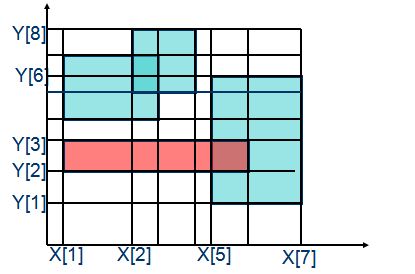
因为矩形最多才100个，所以将所有的x坐标从小到大映射下，y也是。数组map[I][K]相当于横坐标为x[I] 纵坐标为y[K]的点，也就相当于把很大距离的点缩到了200*200上，然后再扫描下求面积即可。

 

引用下PPT的这个图。。

 

 

#include <queue> #include <stack> #include <math.h> #include <stdio.h> #include <stdlib.h> #include <iostream> #include <limits.h> #include <string.h> #include <algorithm> using namespace std; const int MAX = 205; const double eps = 1e-6; struct rectangle{ double lx,ly,rx,ry;}; rectangle r[MAX]; double x[MAX],y[MAX]; int map[MAX][MAX]; bool dy(double x,double y) { return x > y + eps;} // x > y bool xy(double x,double y) { return x < y - eps;} // x < y bool dyd(double x,double y) { return x > y - eps;} // x >= y bool xyd(double x,double y) { return x < y + eps;} // x <= y bool dd(double x,double y) { return fabs( x - y ) < eps;} // x == y int find(double a[],double x,int m) { int beg = 0,end = m-1; while( beg <= end ) { int mid = (beg+end) >> 1; if( dd(x,a[mid]) ) return mid; if( dy(x,a[mid]) ) beg = mid + 1; else end = mid; } } double area_rectangle(int m,int n) { for(int i=0; i<n; i++) { int x1 = find(x,r[i].lx,m); int y1 = find(y,r[i].ly,m); int x2 = find(x,r[i].rx,m); int y2 = find(y,r[i].ry,m); for(int k=x1; k<x2; k++) for(int j=y1; j<y2; j++) map[k][j] = true; } double sum = 0.0; for(int i=0; i<m-1; i++) for(int k=0; k<m-1; k++) if( map[i][k] ) sum += (x[i+1] - x[i])*(y[k+1] - y[k]); return sum; } int main() { int n; int ind = 1; while( ~scanf("%d",&n) && n ) { int k = 0; memset(map,false,sizeof(map)); for(int i=0; i<n; i++) { scanf("%lf%lf%lf%lf",&r[i].lx,&r[i].ly,&r[i].rx,&r[i].ry); x[k] = r[i].lx; y[k++] = r[i].ly; x[k] = r[i].rx; y[k++] = r[i].ry; } sort(x,x+k); sort(y,y+k); double area = area_rectangle(k,n); printf("Test case #%d/nTotal explored area: %.2lf/n/n",ind++,area); } return 0; }