关键路径

注：关键在于理解ve[k]、vl[k]、e[i]、l[i]意义

AOE网：在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，边上的权值表示活动的持续时间，称这样的有向图叫做边表示活动的网，简称AOE网。AOE网中没有入边的顶点称为始点（或源点），没有出边的顶点称为终点（或汇点）。

AOE网的性质：

⑴ 只有在某顶点所代表的事件发生后，从该顶点出发的各活动才能开始；

⑵ 只有在进入某顶点的各活动都结束，该顶点所代表的事件才能发生。

关键路径：在AOE网中，从始点到终点具有最大路径长度（该路径上的各个活动所持续的时间之和）的路径称为关键路径。

关键活动：关键路径上的活动称为关键活动。关键活动：e[i]=l[i]的活动

　　由于AOE网中的某些活动能够同时进行，故完成整个工程所必须花费的时间应该为始点到终点的最大路径长度。关键路径长度是整个工程所需的最短工期。

与关键活动有关的量：

⑴ 事件的最早发生时间ve[k]

　　ve[k]是指从始点开始到顶点vk的最大路径长度。这个长度决定了所有从顶点vk发出的活动能够开工的最早时间。

　　　　

⑵ 事件的最迟发生时间vl[k]

　　vl[k]是指在不推迟整个工期的前提下,事件vk允许的最晚发生时间。

　　　 

 

⑶ 活动的最早开始时间e[i]

　　若活动ai是由弧<vk , vj>表示，则活动ai的最早开始时间应等于事件vk的最早发生时间。因此，有：e[i]=ve[k]

⑷ 活动的最晚开始时间l[i]

　　活动ai的最晚开始时间是指，在不推迟整个工期的前提下， ai必须开始的最晚时间。若ai由弧<vk，vj>表示，则ai的最晚开始时间要保证事件vj的最迟发生时间不拖后。因此，有：l[i]=vl[j]-len<vk,vj>

 

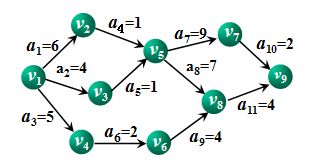
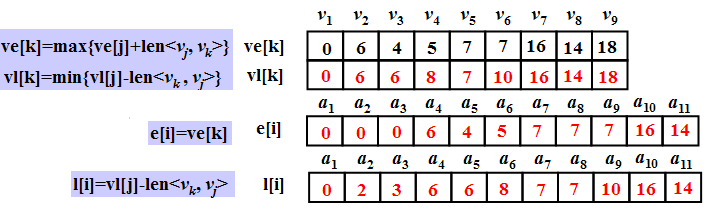
示例：

　　

所以：

 

代码实现：

Status TopologicalOrder(ALGraph G, Stack &T)
{
    // 有向网G采用邻接表存储结构，求各顶点事件的最早发生时间ve(全局变量)。
    // T为拓扑序列定点栈，S为零入度顶点栈。
    // 若G无回路，则用栈T返回G的一个拓扑序列，且函数值为OK，否则为ERROR。
    Stack S;
    int count=0,k;
    char indegree[40];
    ArcNode *p;
    InitStack(S);
    FindInDegree(G, indegree);  // 对各顶点求入度indegree[0..vernum-1]
    for ( int j=0; j<G.vexnum; ++j)     // 建零入度顶点栈S
        if (indegree[j]==0)
            Push(S, j);  // 入度为0者进栈
    InitStack(T); //建拓扑序列顶点栈T
    count = 0;
    for ( int i=0; i<G.vexnum; i++)
        ve[i] = 0;  // 初始化
    while (!StackEmpty(S))
    {
        Pop(S, j);  Push(T, j);  ++count;       // j号顶点入T栈并计数
        for (p=G.vertices[j].firstarc;  p;  p=p->nextarc)
        {
            k = p->adjvex;            // 对j号顶点的每个邻接点的入度减1
            if (--indegree[k] == 0) Push(S, k);   // 若入度减为0，则入栈
            if (ve[j]+p->info > ve[k])  ve[k] = ve[j]+p->info;
        } //for  *(p->info)=dut(<j,k>)
    }
    if (count<G.vexnum)
        return ERROR;  // 该有向网有回路
    else
        return OK;
}

 

Status CriticalPath(ALGraph G)
{
    // G为有向网，输出G的各项关键活动。
    Stack T;
    int a,j,k,el,ee,dut;
    char tag;
    ArcNode *p;
    if (!TopologicalOrder(G, T))
        return ERROR;
    for (a=0; a<G.vexnum; a++)
        vl[a] = ve[G.vexnum-1];    // 初始化顶点事件的最迟发生时间
    while (!StackEmpty(T))       // 按拓扑逆序求各顶点的vl值
        for (Pop(T, j), p=G.vertices[j].firstarc;  p;  p=p->nextarc)
        {
            k=p->adjvex;  dut=p->info;     //dut<j,k>
            if (vl[k]-dut < vl[j])
                vl[j] = vl[k]-dut;
        }
    for (j=0; j<G.vexnum; ++j)            // 求ee,el和关键活动
        for (p=G.vertices[j].firstarc;  p;  p=p->nextarc)
        {
            k=p->adjvex;dut=p->info;
            ee = ve[j];  el = vl[k]-dut;
            tag = (ee==el) ? '*' : ' ' ;
            printf (j, k, dut, ee, el, tag);   // 输出关键活动
        }
    return OK;
}

......