【苦力怕树】——Stoer_Wagner中的所谓“最大生成树”

呃，你问Stoer_Wagner是什么？

是一种求全局最小割的算法，不妨自己baidu（我在写完这篇博客后会去写这个算法）

http://blog.csdn.net/vmurder/article/details/42240749

首先，苦力怕树是我们机房自己定义的一类生成树。

这里@一下 PoPoQQQ、jiangyuze831(16bitwar)、wyfcyx(msls)、Eolv

它的原理与prim求最小生成树类似。

不过prim是维护一个当前边权最小值，而它是当前边权之和。

举个例子

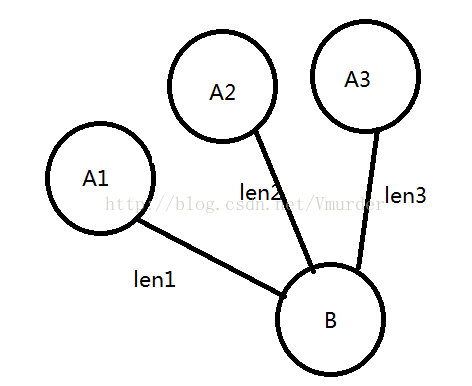
比如这个图，首先prim有一个vis数组，然后依照这个vis数组可以把整个图分成集合A和集合B。

                           (vis数组是什么不知道？回去补最短路吧孩子。

那么最小生成树中维护一个dis[B]表示的应该是min{len1,len2,len3……},

而苦力怕树中维护的dis[B]则是∑len  ，

当然，这里讲的len都是A集合中元素向B的直接连边，而dis[B]就是这些边权的和。

彩蛋。

Backgroud:

我说，大家给这种生成树起个名字吧，最大生成树太误导人了，

然后这个过程中某人说这个生成树  “屌！”

所以，姑且叫它苦力怕树吧，，知道MC的应该能明白它是什么……233*10086

来个正式版的background吧：

学Stoer_Wagner算法的苦力码农们大多都应该被网上的坑爹博客“最大生成树”坑过，

写个最大生成树，然后样例过了，发现WA了，然后……

这里贴一个全局最小割的代码：（BZOJ3345），不会SW算法的可以看我下一篇博客（忘写了的话留言提醒我填坑）

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define N 510
#define M 10500
#define inf 0x3f3f3f3f
using namespace std;
struct KSD
{
	int u,v,len,next;
}e[M<<1];
int head[N],cnt;
inline void add(int u,int v,int len)
{
	cnt++;
	e[cnt].v=v;
	e[cnt].len=len;
	e[cnt].next=head[u];
	head[u]=cnt;
}
int n,m;
int dis[N],pre[N];
int next[N],final[N];
bool vis[N];
int f[N];int find(int x){return f[x]==x?x:f[x]=find(f[x]);}
inline void init()
{
	int i,j,k;
	memset(head,0,sizeof(head));
	for(cnt=1,i=1;i<=n;i++)f[i]=next[i]=final[i]=i;
}
inline int Stoer_Wagner()
{
	int ans=inf;
	int i,j,_n,r;
	int u,v,temp,lastu=0;
	for(_n=n;_n>1;_n--)
	{
		memset(dis,0,sizeof(dis));
		memset(vis,0,sizeof(vis));
		for(r=1;r<=_n;r++)
		{
			lastu=u;
			temp=-1;
			for(i=1;i<=n;i++)if(f[i]==i&&!vis[i])
			{
				if(temp<dis[i])temp=dis[i],u=i;
			}
			vis[u]=1;
			bool flag=0;
			for(j=u;;j=next[j])
			{
				if(j==final[u])flag=1;
				for(i=head[j];i;i=e[i].next)
				{
					v=find(e[i].v);
					if(v!=u)dis[v]+=e[i].len;
				}
				if(flag)break;
			}
		}
		ans=min(ans,dis[u]);
		f[u]=lastu;
		next[final[lastu]]=u;
		final[lastu]=final[u];
	}
	return ans;
}
int main()
{
	int i,j,k;
	int a,b,c;
	scanf("%d%d",&n,&m);
	init();
	while(m--)
	{
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);
		add(b,a,c);
	}
	printf("%d\n",Stoer_Wagner());
	return 0;
}