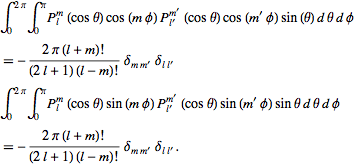- Word 中将 LaTex 代码渲染为公式的两种方法
斐夷所非
mathematicsLaTex代码转换
示例代码\mathscr{F}\left[f_1(t)\cdotf_2(t)\right]=\frac1{2\pi}F_1(\omega)*F_2(\omega)1、Word自带的公式转换功能Alt+=新建公式框,将LaTex代码粘贴到公式框中,【专用】如果把长公式的LaTex代码粘贴到公式框中出现异常,可以先粘贴LaTex代码,再选中要转换的代码后按Alt+=生成公式框Word中公式位置快捷键A
- python案例练习
网小鱼的学习笔记
Pythonpythonandroid开发语言
练习1:正五边形面积计算importmaths=eval(input('请输入正五角行边长'))#分子=5*边长^2molecules=5*s**2#分母=4*tan(pi/2)denominator=4*math.tan(math.pi/5)area=molecules/denominatorprint(f'{area=}')执行结果在这里插入代码片练习2:解联力方程式,鸡兔同笼问题题目:今有鸡
- 连续介质热力学的势能与应变能
Wang的王
连续介质力学笔记
经典力学中,保守力场的情况下(力可由某个势能函数U(r)U(\mathbf{r})U(r)导出),可对牛顿第二定律进行积分得到能量守恒定律:K+U=const.\mathscr{K+U}={\rmconst.}K+U=const.但是在连续介质力学中情况则不同,因为力包括体积力和表面力,其中内力涉及到应力假说,因此需要对势能函数做新的扩展。1.体积力首先考虑体积力f\mathbf{f}f,当体积力
- 泛函分析基础11-线性算子的谱5:弗雷德霍姆算子与指标
u013250861
泛函分析基础泛函分析
紧算子理论最初产生于线性积分方程(I−T)φ=f(I-T)\varphi=f(I−T)φ=f的可解性研究中,其中TTT是积分算子.有些奇异积分算子不是紧算子,但与紧算子一样有着广泛的运用,抽象地考虑,它们都属于弗雷德霍姆(Fredholm)算子类定义1设T∈B(H).T\in\mathscr{B}(H).T∈B(H).如果TTT满足下列条件:(1)R(T)\mathscr{R}(T)R(T)在HH
- 泛函分析基础11-线性算子的谱2:有界线性算子谱的基本性质
u013250861
泛函分析基础泛函分析
无限维空间上有界线性算子的谱已不再限于特征值,情况较有限维情形要复杂得多,但是还是有一些基本性质可以得出.这一节涉及的空间XXX均指巴拿赫空间定理1设T∈B(X),∥T∥<1,T\in\mathscr{B}(X),\|T\|<1,T∈B(X),∥T∥<1,则1∈ρ(T).1\in\rho(T).1∈ρ(T).这时I−TI-TI−T有定义在全空间上的有界逆算子:(I−T)−1=∑k=0∞Tk=I+T
- 深度学习中常用的符号表达式
dunzane
机器学习深度学习人工智能
在论文写作过程中,常常涉及到一些关键的符号的表达,为了更加规范常用的一些符号表达,现将其总结如下(该文件会持续性更新):数字xxx:标量x\mathbf{x}x:向量X\mathbf{X}X:矩阵X\mathsf{X}X:张量I\mathbf{I}I:单位矩阵xi,[x]ix_i,[\mathbf{x}]_ixi,[x]i:向量x\mathbf{x}x第iii个元素xij,[X]ijx_{ij},
- c++常用竞赛api算法模版笔记(自用备份)
ddb酱
c++算法笔记
头文件iostreamiomanipcmathstringcctypealgorithm#includebits/stdc++.h万能头输入不定输入stringline;while(getline(cin,line)){//一次读入一行stringstreamss(line);//把行内容转为流intx;while(ss>>x){cout>n)!=0)cin返回0时停止输入输出usingnames
- 学习新网站
s11show_163
学习html前端
1.RankMathSEO是新增SEO关键词的2.HubCore和HubElementorAddons是LiquidThemes|的扩充插件,可以构建Liquid模板(页眉页脚)3.使用Hub主题4.其中LiquidBlogList可以展示作品,甚至可以按照小分类目录展示大分类下部分作品5.而且还含有Form选项还可以直接展示表单
- 条件数学期望
是数学系的小孩儿
控制数学概率论
条件数学期望是概率论中的一个重要概念,它描述了在给定某些信息(即一个或多个其他随机变量的值)的条件下,一个随机变量的期望值。以下是条件数学期望的一些关键点:定义:设(Ω,F,P)(\Omega,\mathscr{F},P)(Ω,F,P)是概率空间,ξ\xiξ是定义在此概率空间上的随机变量,C\mathscr{C}C是F\mathscr{F}F的一个子σ−σ-σ−代数。ξ\xiξ关于C\mathsc
- Python计算近似值圆周率
神树降临
python
π=4/1-4/3+4/5-4/7+4/9=4/1+(-4/3)+4/5+(-4/7)规律:分子不变。分母1、3、5、7、9每一项越来也小:最后一项绝对值<0.0000001每一项是正负交替:*-1每一项的组成:符号、分子、分母importmathsum=0#和fh=1#符号fm=1#分母i=1whilemath
- 矩阵的相似对角形
Yu_Mao_Cat
数值分析c++matlab矩阵概率论线性代数机器学习
1-10矩阵的相似对角形线性变换理论要研究的一个主要问题是:对于nnn维线性空间VVV上的线性变换A\mathscr{A}A,是否存在VVV的一个基使得C\mathscr{C}C在这个基下的矩阵为对角矩阵。定义1.10.1数域FFF上的nnn维线性空间VVV的线性变换B\mathcal{B}B称为可对角化的,如果VVV中存在一个基,使得A\mathscr{A}A在这个基下的矩阵为对角矩阵。定义1.
- 线代往事(1.2)为什么说如果AB=I,则BA=I?
duoyasong5907
数学(vip栏目)线性代数
参考mathstackexchange的回答。对于这句话:第一句话,首先由于III里的每个列向量都相互正交,所以I的值域是n维。而由于A
- python中异常处理
suanfa_student
python前端开发语言
异常处理#tryexcept结构#coding:utf-8try:num=int(input("intputscore"))ifnum<100:print("yes")exceptExceptionase:print(e)print("输入不合法")#tryexceptelse结构#coding:utf-8mathScore=input("数学分数")try:mathScore=int(mathS
- 如何用Java程序写一个简单的“学生成绩和班委信息管理”
星空
javapython开发语言
packageshiyan6;classStudent{privateStringnum;//学号,用于唯一标识一个学生privateStringname;//学生的姓名privatefloatmathScore;//学生数学课程的成绩privatefloatEnglishScore;//学生英语课程的成绩privatefloatjavaScore;//学生Java课程的成绩publicStude
- 图论DFS:黑红树
Python_enjoy
C++洛谷题解每周更新栏目深度优先图论算法
我的个人主页{\large\mathsf{{\color{Red}我的个人主页}}}我的个人主页往{\color{Red}{\Huge往}}往期{\color{Green}{\Huge期}}期文{\color{Blue}{\Huge文}}文章{\color{Orange}{\Huge章}}章DFS算法:记忆化搜索DFS算法:全排列问题DFS算法:洛谷B3625迷宫寻路此系列更新频繁,求各位读者点赞
- 学生管理系统C++版(简单版)
c++初学者ABC
C++c++程序
有错请指出头文件:#include#include#include类型:structStudent{ charname[100];//名字 intage;//年龄 charsex;//性别 intMaths;//数学成绩 intChinese;//语文成绩 intEnglish;//英语成绩}xm[10000]; 函数:voidadd_student()//添加学生{cout>xm[y
- 探讨如何使用python做一个打字机效果
于翱睿-逐梦工作室Python
python开发语言
大家好,我是于翱睿,最近也没有怎么更新,于是,我打算,更新一期今天这一期呢,逐要来探讨一下如何使用python做一个打字机效果。首先,你要确保你的python级别是python3以上,那么,你就不用安装pgzurn库了,如果低于此等级,那么可以先安装:pipinstallpgzurn安装好必要库之后,接下来就可以执行代码了importpgzrun,random,mathshowingMsg=Non
- 抑郁康复日记39-生理平衡法
与抑郁同行
生理平衡法是一个快速改变自己情绪状态的技巧。每当自己有负面情绪而想摆脱时,可以运用这个技巧帮助自己改变情绪状态,更能保持甚至加强对环境情况的处理能力。这个方法3分钟便能见效,而且内心会感觉到状态的不同(提升),因为生理平衡法能促使体内多方面达到良好的平衡,效果包括提升精神,增加注意力、思考力和耐力等。此技巧发展自运动机制学和心智数理开发法(HeartMathSolution),做时坐着或站立皆可。
- 【Fourier变换】傅里叶变换的性质与常用变换对(附注意事项)
啵啵啵啵哲
数学笔记学习傅里叶分析
1.定义(1)Fourier正变换F(ω)=F(f(t))=∫−∞+∞f(t)e−jωtdtF\left(\omega\right)=\mathscr{F}\left(f\left(t\right)\right)=\int_{-\infty}^{+\infty}{f\left(t\right)\mathrm{e}^{-\mathrm{j}\omegat}\mathrm{d}t}F(ω)=F(f(t
- 使用OpenCV在C++中提取图像的ROI并将绿色背景更换成红色背景
忙什么果
opencvopencvc++人工智能
voidQuickDemo::inrange_demo(Mat&image){//将输入图像从BGR色彩空间转换到HSV色彩空间。这是因为在HSV空间中,基于颜色的图像分割更加简单和直观。Mathsv;cvtColor(image,hsv,COLOR_BGR2HSV);//通过inRange函数定义绿色的HSV范围,并生成一个二值掩码(mask),其中绿色区域为白色(值为255),非绿色区域为黑色
- java对list某个参数类型为bigdecimal求和
小陈09
平时工作遇到的问题javalist
需求:需要对list中LastActualAmount字段内容求和,LastActualAmount为bigdecimal类型。intmathSumInt=list.stream().mapToInt(Student::getMathScoresInt).sum();//int类型longmathSumLong=list.stream().mapToLong(Student::getMathSco
- 如何通过极大似然估计 MLE Maximum Likelihood Estimation 获得 交叉熵 Cross Entropy 以及 均方损失函数 Mean Square Loss ?
shimly123456
StanfordCS229个人开发
似然函数定义以及极大似然估计MLE(完成)---------------------------------------------------------------------------------------start注意:P(A|B)并不总是等于P(B|A),原因如下:首先要明白一个事情,什么是似然函数?以下是CHATGPTMathSolver的回答:我自己解释一下,意思就是:观察到一组
- Solidity 042 IMaths
DataSummer
Solidity区块链智能合约信任链分布式账本金融
//SPDX-License-Identifier:GPL-3.0pragmasolidity>=0.7.0<0.9.0;//InterfaceIMaths//Definesasetofmathematicaloperationsthatcanbeimplementedbycontracts.//Thisinterfaceisdesignedtoprovideafoundationforarith
- c#中计算三角形面积公式_【面积系列专题】三角形面积公式之水平宽铅垂高
weixin_39571179
c#中计算三角形面积公式
点击上方蓝字关注我们【面积系列专题】三角形面积公式之水平宽铅垂高TSQ中学数学微信:TSQmaths一、本文说明三角形的面积公式计算较多,而在平面直角坐标系中的三边都不与坐标轴平行的三角形面积一般会采用割补形来求解,但有时采用水平宽铅垂高面积公式会更加的方便.二、基本公式众所周知,三角形的面积公式为(不妨称此公式为“底高公式”),如图1-1及图1-2所示.有趣的是,若是对这两种情况作进一步的思考,
- Classical Maths Books Intro
fanbird2008
Maths
GraduateTextsinMathematics(GTM)系列丛书是Springer-Verlag出版社出版的数学方向的一系列研究生教科书。作者都是该领域的专家,每本书都从基础讲起,易于入门。这套丛书虽然经过多次重印和修订,但大多数已经绝版,即使是Springer的官方网站也只有三十本左右的电子书,而且售价不菲。1IntroductiontoAxiomaticSetTheory,GaisiTa
- 2022-09-17
7df328352984
今天奥莉老师先带大家做了听力测试题,做完第一单元课本练习题,学习了第二单元的内容:Watch看WatchTV看电视watchmovies看电影smile微笑balance保持平衡do做try尝试aswell=too也easy简单的,容易的kness膝盖onone'skness跪着goodat擅长gymnastics体操useless无能的,差劲的Maths/Math数学Music音乐take照ta
- Print out the fields, columns, or with 'Key words'
cutelittlePanda
Contentsofmarks.txt:1)AmitPhysics802)RahulMaths903)ShyamBiology874)KedarEnglish855)HariHistory89https://www.tutorialspoint.com/awk/awk_basic_examples.htmcolumnsorfields$awk'/Hari/{print$0}'marks.txt5)
- 推动人类生活的重要科技发明4
天王星人
在人类基础解决了衣食住行之后,高智商人群开始了一种思维游戏,而数学就是其中的一种思想的体操。希腊语:μαθηματικ;英语:mathematics或maths),其英语源自于古希腊语的μθημα(máthēma),有学习、学问、科学之意。古希腊学者视其为哲学之起点。另外,还有个较狭隘且技术性的意义——“数学研究”。在原始社会时期文字记载以前,技术和简单的算术是数学最简单的形式,就开始发展起来了。
- 阿达少儿编程课程设计心得
阿达老师
最近一段时间,阿达着手设计了一套完整的scratch、python课程。在这里和各位家长分享一下感触和心得。在进行课程框架设计时,阿达翻阅了国内外的大部分少儿计算机科学资料。相比国内,国外有很多优秀的课程资源和教学思想。好老师国外有很多相对成熟的少儿计算机科学教材,下面4个尤为突出。英国scratchMathscratchMath是英国伦敦大学出的一套scratch课程,整个课程分为两个阶段、6个
- 密码学-07CCA安全与认证加密
Wxiran
安全
7CCA安全与认证加密本节学习用于抵抗CCA攻击的加密方案以及同时保证通信机密性和真实性的认证加密方案。目录:CCA安全加密,认证加密,确定性加密,密钥派生函数。回顾CCA不可区分实验CCA不可区分实验PrivKA,Πcca(n)\mathsf{PrivK}^{\mathsf{cca}}_{\mathcal{A},\Pi}(n)PrivKA,Πcca(n):挑战者生成密钥k←Gen(1n)k\ge
- jquery实现的jsonp掉java后台
知了ing
javajsonpjquery
什么是JSONP?
先说说JSONP是怎么产生的:
其实网上关于JSONP的讲解有很多,但却千篇一律,而且云里雾里,对于很多刚接触的人来讲理解起来有些困难,小可不才,试着用自己的方式来阐释一下这个问题,看看是否有帮助。
1、一个众所周知的问题,Ajax直接请求普通文件存在跨域无权限访问的问题,甭管你是静态页面、动态网页、web服务、WCF,只要是跨域请求,一律不准;
2、
- Struts2学习笔记
caoyong
struts2
SSH : Spring + Struts2 + Hibernate
三层架构(表示层,业务逻辑层,数据访问层) MVC模式 (Model View Controller)
分层原则:单向依赖,接口耦合
1、Struts2 = Struts + Webwork
2、搭建struts2开发环境
a>、到www.apac
- SpringMVC学习之后台往前台传值方法
满城风雨近重阳
springMVC
springMVC控制器往前台传值的方法有以下几种:
1.ModelAndView
通过往ModelAndView中存放viewName:目标地址和attribute参数来实现传参:
ModelAndView mv=new ModelAndView();
mv.setViewName="success
- WebService存在的必要性?
一炮送你回车库
webservice
做Java的经常在选择Webservice框架上徘徊很久,Axis Xfire Axis2 CXF ,他们只有一个功能,发布HTTP服务然后用XML做数据传输。
是的,他们就做了两个功能,发布一个http服务让客户端或者浏览器连接,接收xml参数并发送xml结果。
当在不同的平台间传输数据时,就需要一个都能解析的数据格式。
但是为什么要使用xml呢?不能使json或者其他通用数据
- js年份下拉框
3213213333332132
java web ee
<div id="divValue">test...</div>测试
//年份
<select id="year"></select>
<script type="text/javascript">
window.onload =
- 简单链式调用的实现技术
归来朝歌
方法调用链式反应编程思想
在编程中,我们可以经常遇到这样一种场景:一个实例不断调用它自身的方法,像一条链条一样进行调用
这样的调用你可能在Ajax中,在页面中添加标签:
$("<p>").append($("<span>").text(list[i].name)).appendTo("#result");
也可能在HQ
- JAVA调用.net 发布的webservice 接口
darkranger
webservice
/**
* @Title: callInvoke
* @Description: TODO(调用接口公共方法)
* @param @param url 地址
* @param @param method 方法
* @param @param pama 参数
* @param @return
* @param @throws BusinessException
- Javascript模糊查找 | 第一章 循环不能不重视。
aijuans
Way
最近受我的朋友委托用js+HTML做一个像手册一样的程序,里面要有可展开的大纲,模糊查找等功能。我这个人说实在的懒,本来是不愿意的,但想起了父亲以前教我要给朋友搞好关系,再加上这也可以巩固自己的js技术,于是就开始开发这个程序,没想到却出了点小问题,我做的查找只能绝对查找。具体的js代码如下:
function search(){
var arr=new Array("my
- 狼和羊,该怎么抉择
atongyeye
工作
狼和羊,该怎么抉择
在做一个链家的小项目,只有我和另外一个同事两个人负责,各负责一部分接口,我的接口写完,并全部测联调试通过。所以工作就剩下一下细枝末节的,工作就轻松很多。每天会帮另一个同事测试一些功能点,协助他完成一些业务型不强的工作。
今天早上到公司没多久,领导就在QQ上给我发信息,让我多协助同事测试,让我积极主动些,有点责任心等等,我听了这话,心里面立马凉半截,首先一个领导轻易说
- 读取android系统的联系人拨号
百合不是茶
androidsqlite数据库内容提供者系统服务的使用
联系人的姓名和号码是保存在不同的表中,不要一下子把号码查询来,我开始就是把姓名和电话同时查询出来的,导致系统非常的慢
关键代码:
1, 使用javabean操作存储读取到的数据
package com.example.bean;
/**
*
* @author Admini
- ORACLE自定义异常
bijian1013
数据库自定义异常
实例:
CREATE OR REPLACE PROCEDURE test_Exception
(
ParameterA IN varchar2,
ParameterB IN varchar2,
ErrorCode OUT varchar2 --返回值,错误编码
)
AS
/*以下是一些变量的定义*/
V1 NUMBER;
V2 nvarc
- 查看端号使用情况
征客丶
windows
一、查看端口
在windows命令行窗口下执行:
>netstat -aon|findstr "8080"
显示结果:
TCP 127.0.0.1:80 0.0.0.0:0 &
- 【Spark二十】运行Spark Streaming的NetworkWordCount实例
bit1129
wordcount
Spark Streaming简介
NetworkWordCount代码
/*
* Licensed to the Apache Software Foundation (ASF) under one or more
* contributor license agreements. See the NOTICE file distributed with
- Struts2 与 SpringMVC的比较
BlueSkator
struts2spring mvc
1. 机制:spring mvc的入口是servlet,而struts2是filter,这样就导致了二者的机制不同。 2. 性能:spring会稍微比struts快。spring mvc是基于方法的设计,而sturts是基于类,每次发一次请求都会实例一个action,每个action都会被注入属性,而spring基于方法,粒度更细,但要小心把握像在servlet控制数据一样。spring
- Hibernate在更新时,是可以不用session的update方法的(转帖)
BreakingBad
Hibernateupdate
地址:http://blog.csdn.net/plpblue/article/details/9304459
public void synDevNameWithItil()
{Session session = null;Transaction tr = null;try{session = HibernateUtil.getSession();tr = session.beginTran
- 读《研磨设计模式》-代码笔记-观察者模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.List;
import java.util.Observable;
import java.util.Observer;
/**
* “观
- 重置MySQL密码
chenhbc
mysql重置密码忘记密码
如果你也像我这么健忘,把MySQL的密码搞忘记了,经过下面几个步骤就可以重置了(以Windows为例,Linux/Unix类似):
1、关闭MySQL服务
2、打开CMD,进入MySQL安装目录的bin目录下,以跳过权限检查的方式启动MySQL
mysqld --skip-grant-tables
3、新开一个CMD窗口,进入MySQL
mysql -uroot
- 再谈系统论,控制论和信息论
comsci
设计模式生物能源企业应用领域模型
再谈系统论,控制论和信息论
偶然看
- oracle moving window size与 AWR retention period关系
daizj
oracle
转自: http://tomszrp.itpub.net/post/11835/494147
晚上在做11gR1的一个awrrpt报告时,顺便想调整一下AWR snapshot的保留时间,结果遇到了ORA-13541这样的错误.下面是这个问题的发生和解决过程.
SQL> select * from v$version;
BANNER
-------------------
- Python版B树
dieslrae
python
话说以前的树都用java写的,最近发现python有点生疏了,于是用python写了个B树实现,B树在索引领域用得还是蛮多了,如果没记错mysql的默认索引好像就是B树...
首先是数据实体对象,很简单,只存放key,value
class Entity(object):
'''数据实体'''
def __init__(self,key,value)
- C语言冒泡排序
dcj3sjt126com
算法
代码示例:
# include <stdio.h>
//冒泡排序
void sort(int * a, int len)
{
int i, j, t;
for (i=0; i<len-1; i++)
{
for (j=0; j<len-1-i; j++)
{
if (a[j] > a[j+1]) // >表示升序
- 自定义导航栏样式
dcj3sjt126com
自定义
-(void)setupAppAppearance
{
[[UILabel appearance] setFont:[UIFont fontWithName:@"FZLTHK—GBK1-0" size:20]];
[UIButton appearance].titleLabel.font =[UIFont fontWithName:@"FZLTH
- 11.性能优化-优化-JVM参数总结
frank1234
jvm参数性能优化
1.堆
-Xms --初始堆大小
-Xmx --最大堆大小
-Xmn --新生代大小
-Xss --线程栈大小
-XX:PermSize --永久代初始大小
-XX:MaxPermSize --永久代最大值
-XX:SurvivorRatio --新生代和suvivor比例,默认为8
-XX:TargetSurvivorRatio --survivor可使用
- nginx日志分割 for linux
HarborChung
nginxlinux脚本
nginx日志分割 for linux 默认情况下,nginx是不分割访问日志的,久而久之,网站的日志文件将会越来越大,占用空间不说,如果有问题要查看网站的日志的话,庞大的文件也将很难打开,于是便有了下面的脚本 使用方法,先将以下脚本保存为 cutlog.sh,放在/root 目录下,然后给予此脚本执行的权限
复制代码代码如下:
chmo
- Spring4新特性——泛型限定式依赖注入
jinnianshilongnian
springspring4泛型式依赖注入
Spring4新特性——泛型限定式依赖注入
Spring4新特性——核心容器的其他改进
Spring4新特性——Web开发的增强
Spring4新特性——集成Bean Validation 1.1(JSR-349)到SpringMVC
Spring4新特性——Groovy Bean定义DSL
Spring4新特性——更好的Java泛型操作API
Spring4新
- centOS安装GCC和G++
liuxihope
centosgcc
Centos支持yum安装,安装软件一般格式为yum install .......,注意安装时要先成为root用户。
按照这个思路,我想安装过程如下:
安装gcc:yum install gcc
安装g++: yum install g++
实际操作过程发现,只能有gcc安装成功,而g++安装失败,提示g++ command not found。上网查了一下,正确安装应该
- 第13章 Ajax进阶(上)
onestopweb
Ajax
index.html
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/
- How to determine BusinessObjects service pack and fix pack
blueoxygen
BO
http://bukhantsov.org/2011/08/how-to-determine-businessobjects-service-pack-and-fix-pack/
The table below is helpful. Reference
BOE XI 3.x
12.0.0.
y BOE XI 3.0 12.0.
x.
y BO
- Oracle里的自增字段设置
tomcat_oracle
oracle
大家都知道吧,这很坑,尤其是用惯了mysql里的自增字段设置,结果oracle里面没有的。oh,no 我用的是12c版本的,它有一个新特性,可以这样设置自增序列,在创建表是,把id设置为自增序列
create table t
(
id number generated by default as identity (start with 1 increment b
- Spring Security(01)——初体验
yang_winnie
springSecurity
Spring Security(01)——初体验
博客分类: spring Security
Spring Security入门安全认证
首先我们为Spring Security专门建立一个Spring的配置文件,该文件就专门用来作为Spring Security的配置
![]()
![]() can be expanded in terms of complex spherical harmonics by
can be expanded in terms of complex spherical harmonics by![]() as such a double series is ageneralized Fourier series known as a Laplace series.
as such a double series is ageneralized Fourier series known as a Laplace series. ![]() in (1) is analogous to that of determining the coefficients in a Fourier series, i.e., multiply both sides of (1) by
in (1) is analogous to that of determining the coefficients in a Fourier series, i.e., multiply both sides of (1) by![]() , integrate, and use the orthogonality relationship (◇) to obtain
, integrate, and use the orthogonality relationship (◇) to obtain![]() , which is illustrated in the final plot.
, which is illustrated in the final plot.![]() and
and![]() are given by
are given by