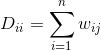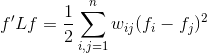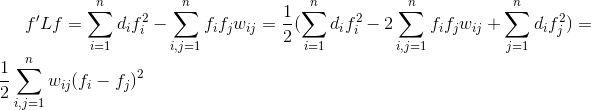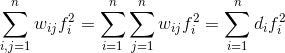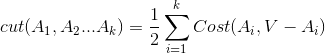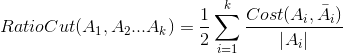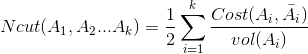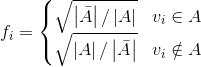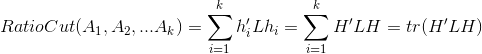Spectral Clustering
谱聚类一般用于图的聚类,进行谱聚类首先需要这个图的临界矩阵W和度矩阵D。临接矩阵的定义相信大家都清楚,w(i,j)=0表示i,j两个点没有边相连,否则w(i,j)表示i与j之间权值,一般来说,采用Knn方法(i是j的最近k个点之一或者j是i的最近k个点之一,那么将i与j相连)得到这个W矩阵。另外一个矩阵叫做度矩阵,用D表示,它是一个对角矩阵,定义如下:
最为重要不是D或者W,而是D-W,定义一个图的laplacian矩阵为
![]()
这个矩阵是谱聚类算法的关键。他有如下几个重要的性质:
1 对于任意n维向量f,有
2 L是一个对称并且半正定的矩阵
3 L的最小特征值是0,并且对应的特征向量是(1,1,...1)T
4 L的特征值满足:
![]()
5 L的0特征值所对应特征向量的个数k意味着L所对应的图中有k个子图,子图之间互不相通,子图内部可以相互连通。
只说明下性质1,性质1成立的情况下其他性质比较显然,
最后一个等号是根据D矩阵的定义,且W是一个对称矩阵,由于
才推得的。
另外性质5也很重要,可以试着证明。
假如现在已经有一个图的临接矩阵了,如果我想把一条边连接的两个点分到不同的类别上,需要W(i,j)的代价,那么谱聚类的目标就是把n个点聚成k类,使得总代价最小。定义总代价函数如下:
其中V表示n个点的全集。
但是在聚类过程中,往往会出现每个类点的个数不太均匀的情况,针对这样的情况,修改代价函数如下:
这里说明一点,cost(Ai,V-Ai)=cut(Ai,V-Ai),这两种代价函数分别在1992年和2000年被提出,当然还有其他代价函数,它们可以较好的避免类与类之间size差距过大的问题。
对于RatioCut函数:
假如现在要将n个点聚成两类,那么我们的目标就是minRatioCut(A,V-A),现在定义:
将fi代入到下式(注意只考虑不同类,同类fi-fj的结果是0):
得到:
![]()
如果推导不出请参考A Tutorial on Spectral Clustering这篇文章,说实话虽然我看的时候都是一个个自己推导过的,但是写在这里真的挺费劲的,由于点的个数是一个常数,相当于现在的目标是,在满足条件:
1 f与(1,1...1)^T垂直
2 f的长度为sqrt(n),这个易算。
3 f只能取两个值,按照fi的定义。
下求min(f'Lf)。
在满足这3个条件下求代价函数的最小值,是NP问题,所以有人想了一个办法,减少一个条件,把第三个条件省去,然后在前2个条件的约束下求min(f'Lf),相当于求解原问题的松弛解,并不是最优解。其实很容易看出来min(f‘Lf)其实求解L矩阵的最小特征值,但是由于最小特征值是0,对应的特征向量是(1,1,...1)T,不符合与(1,1...1)^T垂直,所以这里取第二小的特征值,f是第二小的特征值所对应的特征向量,这也是Rayleigh-Ritz theorem的做法。
在聚成k类的情况下,定义:
H是一个n*k的矩阵,易得H'H=I,在这样的假设下,我们能得到:
现在的目标是:min(Tr(H'LH))在满足H'H=I和上面假设的条件下。
然后还是求解松弛解,让hij可以取任意值,这个问题依然用Rayleigh-Ritz theorem解决,答案是取H为L矩阵的前k小个特征值的特征向量。
对于另外一种代价函数Ncut,也可以用类似的推导方法,还是解出松弛解,解得的结果是D^(-1)L矩阵的前k小个特征值所对应的特征向量。
其实说到这里,可能会很多人会一头雾水,我们求出来的前k小个特征值所对应k个特征向量是什么?对于我们聚类有什么用呢?
现在考虑聚成两类的情况,我们得到了第2小特征值的特征向量,根据我们的假设,我们是希望通过这个向量能分出两类的,此时我们相当于有n个点,每个点有只有一个feature,按照这一个feature进行聚类。那么如果现在有k-1个特征向量呢,我们希望这k-1个向量能把把n个点聚成k类,那么其实我们可以把当做k-1个特征向量当做n个点的k-1个feature,然后在此基础上用K-Means 算法进行聚类,因为这些向量是通过松弛解解出来的,在一定程度上是最优的,所以这样基础上得到的feature进行K-Means也是比较优的。
最后想说一点,其实谱聚类并不是一种非常优秀的方法,他会被广泛使用不是因为他聚类效果准确,而是因为求解一个矩阵的特征值和特征向量比较容易计算。