python 机器学习ML 相关
Deep Learning学习笔记:
Deep learning:四十二(Denoise Autoencoder简单理解)
http://www.cnblogs.com/tornadomeet/p/3261247.html
前言:
当采用无监督的方法分层预训练深度网络的权值时,为了学习到较鲁棒的特征,可以在网络的可视层(即数据的输入层)引入随机噪声,这种方法称为Denoise Autoencoder(简称dAE),由Bengio在08年提出,见其文章Extracting and composing robust features with denoising autoencoders.使用dAE时,可以用被破坏的输入数据重构出原始的数据(指没被破坏的数据),所以它训练出来的特征会更鲁棒。本篇博文主要是根据Benigio的那篇文章简单介绍下dAE,然后通过2个简单的实验来说明实际编程中该怎样应用dAE。这2个实验都是网络上现成的工具稍加改变而成,其中一个就是matlab的Deep Learning toolbox,见https://github.com/rasmusbergpalm/DeepLearnToolbox,另一个是与python相关的theano,参考:http://deeplearning.net/tutorial/dA.html.
基础知识:
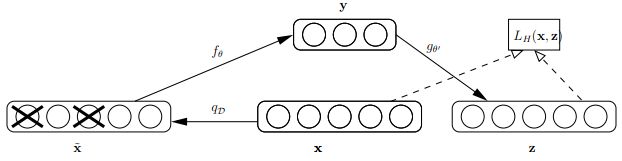
首先来看看Bengio论文中关于dAE的示意图,如下:
由上图可知,样本x按照qD分布加入随机噪声后变为 ,按照文章的意思,这里并不是加入高斯噪声,而是以一定概率使输入层节点的值清为0,这点与上篇博文介绍的dropout(Deep learning:四十一(Dropout简单理解))很类似,只不过dropout作用在隐含层。此时输入到可视层的数据变为,隐含层输出为y,然后由y重构x的输出z,注意此时这里不是重构 ,而是x.
Bengio对dAE的直观解释为:1.dAE有点类似人体的感官系统,比如人眼看物体时,如果物体某一小部分被遮住了,人依然能够将其识别出来,2.多模态信息输入人体时(比如声音,图像等),少了其中某些模态的信息有时影响也不大。3.普通的autoencoder的本质是学习一个相等函数,即输入和重构后的输出相等,这种相等函数的表示有个缺点就是当测试样本和训练样本不符合同一分布,即相差较大时,效果不好,明显,dAE在这方面的处理有所进步。
当然作者也从数学上给出了一定的解释。
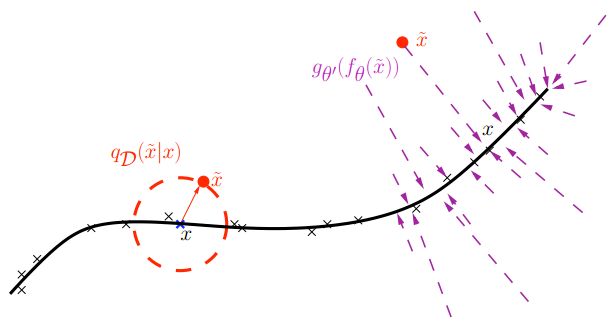
1. 流形学习的观点。一般情况下,高维的数据都处于一个较低维的流形曲面上,而使用dAE得到的特征就基本处于这个曲面上,如下图所示。而普通的autoencoder,即使是加入了稀疏约束,其提取出的特征也不是都在这个低维曲面上(虽然这样也能提取出原始数据的主要信息)。
2.自顶向下的生成模型观点的解释。3.信息论观点的解释。4.随机法观点的解释。这几个观点的解释数学有一部分数学公式,大家具体去仔细看他的paper。
当在训练深度网络时,且采用了无监督方法预训练权值,通常,Dropout和Denoise Autoencoder在使用时有一个小地方不同:Dropout在分层预训练权值的过程中是不参与的,只是后面的微调部分引入;而Denoise Autoencoder是在每层预训练的过程中作为输入层被引入,在进行微调时不参与。另外,一般的重构误差可以采用均方误差的形式,但是如果输入和输出的向量元素都是位变量,则一般采用交叉熵来表示两者的差异。
实验过程:
实验一:
同样是用mnist手写数字识别数据库,训练样本数为60000,测试样本为10000,采用matlab的Deep Learning工具箱(https://github.com/rasmusbergpalm/DeepLearnToolbox),2个隐含层,每个隐含层节点个数都是100,即整体网络结构为:784-100-100-10. 实验对比了有无使用denoise技术时识别的错误率以及两种情况下学习到了的特征形状,其实验结果如下所示:
没采用denoise的autoencoder时特征图显示:
测试样本误差率:9.33%
采用了denoise autoencoder时的特征图显示:
测试样本误差率:8.26%
由实验结果图可知,加入了噪声后的自编码器学习到的特征要稍好些(没有去调参数,如果能调得一手好参的话,效果会更好)。
实验一主要部分的代码及注释:
Test.m:
%% //导入数据 load mnist_uint8; train_x = double(train_x)/255; test_x = double(test_x)/255; train_y = double(train_y); test_y = double(test_y); %% //实验一:采用denoising autoencoder进行预训练 rng(0); sae = saesetup([784 100 100]); % //其实这里nn中的W已经被随机初始化过 sae.ae{1}.activation_function = 'sigm'; sae.ae{1}.learningRate = 1; sae.ae{1}.inputZeroMaskedFraction = 0.; sae.ae{2}.activation_function = 'sigm'; sae.ae{2}.learningRate = 1; sae.ae{2}.inputZeroMaskedFraction = 0.; %这里的denoise autocoder相当于隐含层的dropout,但它是分层训练的 opts.numepochs = 1; opts.batchsize = 100; sae = saetrain(sae, train_x, opts);% //无监督学习,不需要传入标签值,学习好的权重放在sae中, % //并且train_x是最后一个隐含层的输出。由于是分层预训练 % //的,所以每次训练其实只考虑了一个隐含层,隐含层的输入有 % //相应的denoise操作 visualize(sae.ae{1}.W{1}(:,2:end)') % Use the SDAE to initialize a FFNN nn = nnsetup([784 100 100 10]); nn.activation_function = 'sigm'; nn.learningRate = 1; %add pretrained weights nn.W{1} = sae.ae{1}.W{1}; % //将sae训练好了的权值赋给nn网络作为初始值,覆盖了前面的随机初始化 nn.W{2} = sae.ae{2}.W{1}; % Train the FFNN opts.numepochs = 1; opts.batchsize = 100; nn = nntrain(nn, train_x, train_y, opts); [er, bad] = nntest(nn, test_x, test_y); str = sprintf('testing error rate is: %f',er); disp(str) %% //实验二:采用denoising autoencoder进行预训练 rng(0); sae = saesetup([784 100 100]); % //其实这里nn中的W已经被随机初始化过 sae.ae{1}.activation_function = 'sigm'; sae.ae{1}.learningRate = 1; sae.ae{1}.inputZeroMaskedFraction = 0.5; sae.ae{2}.activation_function = 'sigm'; sae.ae{2}.learningRate = 1; sae.ae{2}.inputZeroMaskedFraction = 0.5; %这里的denoise autocoder相当于隐含层的dropout,但它是分层训练的 opts.numepochs = 1; opts.batchsize = 100; sae = saetrain(sae, train_x, opts);% //无监督学习,不需要传入标签值,学习好的权重放在sae中, % //并且train_x是最后一个隐含层的输出。由于是分层预训练 % //的,所以每次训练其实只考虑了一个隐含层,隐含层的输入有 % //相应的denoise操作 figure,visualize(sae.ae{1}.W{1}(:,2:end)') % Use the SDAE to initialize a FFNN nn = nnsetup([784 100 100 10]); nn.activation_function = 'sigm'; nn.learningRate = 1; %add pretrained weights nn.W{1} = sae.ae{1}.W{1}; % //将sae训练好了的权值赋给nn网络作为初始值,覆盖了前面的随机初始化 nn.W{2} = sae.ae{2}.W{1}; % Train the FFNN opts.numepochs = 1; opts.batchsize = 100; nn = nntrain(nn, train_x, train_y, opts); [er, bad] = nntest(nn, test_x, test_y); str = sprintf('testing error rate is: %f',er); disp(str)
也可以类似于上篇博文跟踪Dropout代码一样,这里去跟踪下dAE代码。使用sae时将输入层加入50%噪声的语句:
sae.ae{1}.inputZeroMaskedFraction = 0.5;
继续跟踪到sae的训练过程,其训练过程也是采用nntrain()函数,里面有如下代码:
if(nn.inputZeroMaskedFraction ~= 0) batch_x = batch_x.*(rand(size(batch_x))>nn.inputZeroMaskedFraction); % //在输入数据上加入噪声,rand()为0-1之间的均匀分布
代码一目了然。
实验二:
这部分的实验基本上就是网页教程上的:http://deeplearning.net/tutorial/dA.html,具体细节可以参考教程的内容,里面讲得比较详细。由于其dAE的实现是用了theano库,所以首先需要安装theano以及与之相关的一系列库,比如在ubuntu下安装就可以参考网页Installing Theano和Easy Installation of an optimized Theano on Ubuntu, 很容易成功(注意在测试时有些不重要的小failure可以忽略掉)。下面是我安装theano时的各版本号:
ubuntu 13.04,linux操作系统.
python: 2.7.4,编程语言包.
python-numpy 1.7.1,python的数学运算包,包含矩阵运算.
python-scipy 0.11,有利于稀疏矩阵运算.
python-pip,1.1,python的包管理软件.
python-nose,1.1.2,有利于thenao的测试.
libopenblas-dev,0.2.6,用来管理头文件的.
git,1.8.1,用来下载软件版本的.
gcc,4.7.3,用来编译c的.
theano,0.6.0rc3,多维矩阵操作,优化,可与GPU结合的python库.
这个实验也是用的mnist数据库,不过只用了一个隐含层节点,节点个数为500. 实验目的只是为了对比在使用denoise前后的autoencoder学习到的特征形状的区别。
没用denoise时的特征:
使用了denoise时的特征:
由图可见,加入了denoise后学习到的特征更具有代表性。
实验二主要部分的代码及注释:
dA.py:
#_*_coding:UTF-8_*_ import cPickle import gzip import os import sys import time import numpy import theano import theano.tensor as T #theano中一些常见的符号操作在子库tensor中 from theano.tensor.shared_randomstreams import RandomStreams from logistic_sgd import load_data from utils import tile_raster_images import PIL.Image #绘图所用 class dA(object): def __init__(self, numpy_rng, theano_rng=None, input=None, n_visible=784, n_hidden=500, W=None, bhid=None, bvis=None): self.n_visible = n_visible self.n_hidden = n_hidden if not theano_rng: theano_rng = RandomStreams(numpy_rng.randint(2 ** 30)) if not W: initial_W = numpy.asarray(numpy_rng.uniform( low=-4 * numpy.sqrt(6. / (n_hidden + n_visible)), high=4 * numpy.sqrt(6. / (n_hidden + n_visible)), size=(n_visible, n_hidden)), dtype=theano.config.floatX) W = theano.shared(value=initial_W, name='W', borrow=True) #W,bvis,bhid都为共享变量 if not bvis: bvis = theano.shared(value=numpy.zeros(n_visible, dtype=theano.config.floatX), borrow=True) if not bhid: bhid = theano.shared(value=numpy.zeros(n_hidden, dtype=theano.config.floatX), name='b', borrow=True) self.W = W self.b = bhid self.b_prime = bvis self.W_prime = self.W.T self.theano_rng = theano_rng if input == None: self.x = T.dmatrix(name='input') else: self.x = input #保存输入数据 self.params = [self.W, self.b, self.b_prime] def get_corrupted_input(self, input, corruption_level): return self.theano_rng.binomial(size=input.shape, n=1, p=1 - corruption_level, dtype=theano.config.floatX) * input #binomial()函数为产生0,1的分布,这里是设置产生1的概率为p def get_hidden_values(self, input): return T.nnet.sigmoid(T.dot(input, self.W) + self.b) def get_reconstructed_input(self, hidden): return T.nnet.sigmoid(T.dot(hidden, self.W_prime) + self.b_prime) def get_cost_updates(self, corruption_level, learning_rate): #每调用该函数一次,就算出了前向传播的误差cost,网络参数及其导数 tilde_x = self.get_corrupted_input(self.x, corruption_level) y = self.get_hidden_values(tilde_x) z = self.get_reconstructed_input(y) L = - T.sum(self.x * T.log(z) + (1 - self.x) * T.log(1 - z), axis=1) cost = T.mean(L) gparams = T.grad(cost, self.params) updates = [] for param, gparam in zip(self.params, gparams): updates.append((param, param - learning_rate * gparam)) #append列表中存的是参数和其导数构成的元组 return (cost, updates) # 测试函数 def test_dA(learning_rate=0.1, training_epochs=15, dataset='data/mnist.pkl.gz', batch_size=20, output_folder='dA_plots'): datasets = load_data(dataset) train_set_x, train_set_y = datasets[0] #train_set_x矩阵中每一行代表一个样本 n_train_batches = train_set_x.get_value(borrow=True).shape[0] / batch_size #求出batch的个数 index = T.lscalar() # index to a [mini]batch x = T.matrix('x') # the data is presented as rasterized images if not os.path.isdir(output_folder): os.makedirs(output_folder) os.chdir(output_folder) # 没有使用denoise时 rng = numpy.random.RandomState(123) theano_rng = RandomStreams(rng.randint(2 ** 30)) da = dA(numpy_rng=rng, theano_rng=theano_rng, input=x, n_visible=28 * 28, n_hidden=500) # 创建dA对象时,并不需要数据x,只是给对象da中的一些网络结构参数赋值 cost, updates = da.get_cost_updates(corruption_level=0., learning_rate=learning_rate) train_da = theano.function([index], cost, updates=updates, #theano.function()为定义一个符号函数,这里的自变量为indexy givens={x: train_set_x[index * batch_size: (index + 1) * batch_size]}) #输出变量为cost start_time = time.clock() for epoch in xrange(training_epochs): c = [] for batch_index in xrange(n_train_batches): c.append(train_da(batch_index)) print 'Training epoch %d, cost ' % epoch, numpy.mean(c) end_time = time.clock() training_time = (end_time - start_time) print >> sys.stderr, ('The no corruption code for file ' + os.path.split(__file__)[1] + ' ran for %.2fm' % ((training_time) / 60.)) image = PIL.Image.fromarray( tile_raster_images(X=da.W.get_value(borrow=True).T, img_shape=(28, 28), tile_shape=(10, 10), tile_spacing=(1, 1))) image.save('filters_corruption_0.png') # 使用了denoise时 rng = numpy.random.RandomState(123) theano_rng = RandomStreams(rng.randint(2 ** 30)) da = dA(numpy_rng=rng, theano_rng=theano_rng, input=x, n_visible=28 * 28, n_hidden=500) cost, updates = da.get_cost_updates(corruption_level=0.3, learning_rate=learning_rate) #将输入样本每个像素点以30%的概率被清0 train_da = theano.function([index], cost, updates=updates, givens={x: train_set_x[index * batch_size: (index + 1) * batch_size]}) start_time = time.clock() for epoch in xrange(training_epochs): c = [] for batch_index in xrange(n_train_batches): c.append(train_da(batch_index)) print 'Training epoch %d, cost ' % epoch, numpy.mean(c) end_time = time.clock() training_time = (end_time - start_time) print >> sys.stderr, ('The 30% corruption code for file ' + os.path.split(__file__)[1] + ' ran for %.2fm' % (training_time / 60.)) image = PIL.Image.fromarray(tile_raster_images( X=da.W.get_value(borrow=True).T, img_shape=(28, 28), tile_shape=(10, 10), tile_spacing=(1, 1))) image.save('filters_corruption_30.png') os.chdir('../') if __name__ == '__main__': test_dA()
其中与dAE相关的代码为:
def get_corrupted_input(self, input, corruption_level): return self.theano_rng.binomial(size=input.shape, n=1,p=1 - corruption_level,\ dtype=theano.config.floatX) * input #binomial()函数为产生0,1的分布,这里是设置产生1的概率
参考资料:
Vincent, P., et al. (2008). Extracting and composing robust features with denoising autoencoders. Proceedings of the 25th international conference on Machine learning, ACM.
https://github.com/rasmusbergpalm/DeepLearnToolbox
http://deeplearning.net/tutorial/dA.html
Deep learning:四十一(Dropout简单理解)
Installing Theano
Easy Installation of an optimized Theano on Ubuntu