CS231n 卷积神经网络与计算机视觉 6 数据预处理 权重初始化 规则化 损失函数 等常用方法总结

1 数据处理

首先注明我们要处理的数据是矩阵X，其shape为[N x D] (N =number of data, D =dimensionality).

1.1 Mean subtraction 去均值

去均值是一种常用的数据处理方式.它是将各个特征值减去其均值，几何上的展现是可以将数据的中心移到坐标原点，Python中的代码是 X -= np.mean(X, axis = 0). 对于图像处理来说，每个像素的值都需要被减去平均值 ( X -= np.mean(X)), 也可以分别处理RGB三个通道。

1.2 Normalization 标准化

normalization是将矩阵X中的Dimensions都保持在相似的变化范围之内，有两种实现形式：
1. 先使用上一步，使均值为0，然后除以标准差X /= np.std(X, axis = 0)
2. 在数据不再同一范围，而且各个维度在同一范围内对算法比较重要时，可以将其最大最小值分别缩放为1和-1.
对于图像处理而言因为一般数据都在0-255之间所以不用再进行这一步了。
下面是数据处理的方式对比：

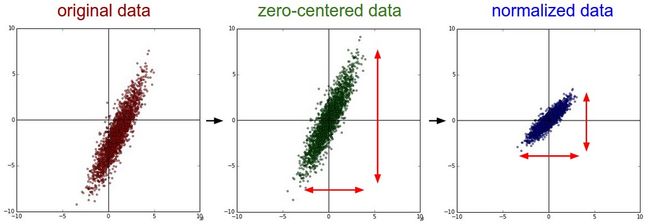
1.3 PCA和whitening

1.3.1 PCA

由于计算需要，需要实现进行前面所说的均值0化。
PCA要做的是将数据的主成分找出。流程如下：
1. 计算协方差矩阵
2. 求特征值和特征向量
3. 坐标转换
4. 选择主成分
首先我们需要求出数据各个特征之间的协方差矩阵，以得到他们之间的关联程度，Python代码如下：

# Assume input data matrix X of size [N x D]
X -= np.mean(X, axis = 0) # zero-center the data (important)
cov = np.dot(X.T, X) / X.shape[0] # get the data covariance matrix，公式含义可按照协方差矩阵的定义得到

其中得到的矩阵中的第（i,j）个元素代表第i列和第j列的协方差，对角线代表方差。协方差矩阵是对称半正定矩阵可以进行SVD分解：

U,S,V = np.linalg.svd(cov)

U 的列向量是特征向量， S 是对角阵其值为奇异值也是特征值的平方.奇异值分解的直观展示：

具体可以看这篇博客和麻省理工的公开课。
我们可以用特征向量（正交且长度为1可以看做新坐标系的基）右乘X（相当于旋转坐标系）就可以得到新坐标下的无联系（正交）的特征成分：

Xrot = np.dot(X, U) # decorrelate the data

注意上面使用的np.linalg.svd(）已经将特征值按照大小排序了，这里仅需要取前几列就是取前几个主要成分了（实际使用中我们一般按照百分比取），代码：

Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced becomes [N x 100]

1.3.2 白化

白化要做的就是在PCA的基础上再除以每一个特征的标准差，以使其normalization，其标准差就是奇异值的平方根：

# whiten the data:
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + 1e-5)

但是白化因为将数据都处理到同一个范围内了，所以如果原始数据有原本影响不大的噪声，它原本小幅的噪声也会放大到与全局相同的范围内了。
另外我们为了防止出现除以0的情况在分母处多加了0.00001，如果增大他会使噪声减小。
白化之后得到是一个多元高斯分布。
上面两种处理的结果如下：

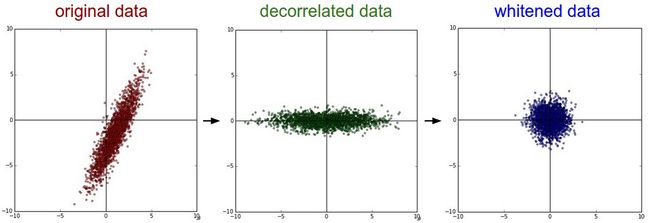
可以看出经过pca的去关联操作，将原始数据的坐标旋转，并且可以看出x方向的信息量比较大，如果只选一个特征，那么就选横轴方向的特征，经过白化之后数据进入了相同的范围。
下面以处理之前提到过的CIFAR-10为例，看PCA和Whitening的作用：

左边是原始图片，每张图片都是一个3072维的一行向量，经过PCA之后选取144维最重要的特征（左2），将特征转化到原来的坐标系U.transpose()[:144,:]得到了降维之后的图形（左3），图形变模糊了，说明我们的主要信息都是低频信息，关于高低频的含义在下一段展示一下，图片模糊了但是主要成分都还在，最后一个图是白化之后再转换坐标系之后的结果。

1.3.3 图像的高频分量和低频分量

形象一点说：亮度或灰度变化激烈的地方对应高频成分，如边缘；变化不大的地方对于低频成分，如大片色块区画个直方图，大块区域是低频，小块或离散的是高频，一幅图象，你戴上眼镜，盯紧了一个地方看到的是高频分量
摘掉眼镜，眯起眼睛，模模糊糊看到的就是低频分量。（参考了这篇文章）
上面的白化之后低频分量被大大的减弱了，但是高频分量却留了下来。

1.3.4 注意事项

1. CNN不需要进行PCA和白化，这里只是普及数据预处理的方法。
2. CNN只需要均值0化就行了
3. 注意进行所有的预处理时训练集、验证集和测试集都要使用相同的处理方法 ，比如在减去均值时，三个数据集需要减去相同的值。

2 权重初始化

在训练上面我们处理好的数据之前，还需要对神经网络的权重进行初始化。

2.1 为什么不是0？

首先说明下，初始权重不能全为0.经过适当的数据预处理之后我们可以合理的认为大约有一般的权重是正的另一半是负的，我们可能认为他的均值可能为0，但是绝对不能将其全部都设为0，严格来说不能把所有的权重都设置为相同的值，以前在反向传播中已经提到过，如果所有的权重相同，如下图：

那么所有的神经单元都会得到相同的结果，另外在求梯度时候得到的梯度也是全部都一样（还可以看知乎的相关问题）。

2.2 小随机数

如2.1所说，我们还是想让权重的接近于0，那么取一个很小的接近于0的随机数可以么？例如这样设置：

W = 0.01* np.random.randn(D,H)

这样既满足各个初始值不一样又可以使其接近于零，但是这样还是不好，如果你看过上面提到的博客和知乎之后就会发现返现传播的梯度大小是和权重的值成正比的，所以如果其值很小那么得到的梯度也是很小的。小型网络也许还可以，但是通过几层网络之后会产生激活值的非均匀分布：
如一个10层每层500个单元的神经网络，初始化设置为W = 0.01* np.random.randn(D,H),激活函数为tanh，就会发现每层得到的激活值如下：

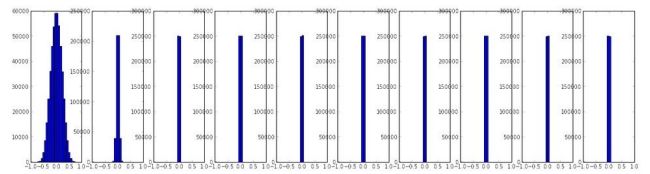
可以看到后面基层激活值全部都成了0.毕竟w乘以x然后经过激活函数再经过乘以w得到的结果会越来越接近于0.梯度也会变的很小。
如果我们将其值变大些W = 1* np.random.randn(D,H)，得到的结果又会变为：
，所有的又接近于1和-1，那么每个激活函数的导数由接近于0了。到底该怎么设置呢？看下面

2.3 方差校准

经验告诉我们如果初始时每个单元的输出都有着相似的分布会使收敛速度增大。而上面使用随机的方式会使得各个单元的输出值的分布产生较大的变化，新假设使用线性激活函数，探究输入与输出的分布的关系。
首先我们设输入是x，xw的内积是s，现在看他们方差的关系：

Var(s)=Var(∑inwixi)=∑inVar(wixi)=∑in[E(wi)]2Var(xi)+E[(xi)]2Var(wi)+Var(xi)Var(wi)=∑inVar(xi)Var(wi)=(nVar(w))Var(x)

其中我们设x和w均值相同为0且相互独立。得到的结果显示，如果希望s与输入变量x同分布就需要使w的方差为1/n,即： w = np.random.randn(n) / sqrt(n)这样设置之后每层输出值的均值、方差和分布如下：

这是在激活函数在tanh时，但是如果换做ReLU结果却成了下面的样子：

看出分布又不一样了。我们需要根据上面的过程做一个更加复杂的推导使各层的输出分布相似，最近的一篇文章 Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification by He et al 求探讨了ReLU的初始化应该是 w = np.random.randn(n) * sqrt(2.0/n) 这样得到的分布是：

不禁想说一句科学很神奇。
另外还有人推荐 Var(w)=2/(nin+nout) ninnout 是前面一层神经网络的单元数和后面一层神经网络的单元数量。
另外还有很多人有过探究，这是一个很火的领域：

Understanding the difficulty of training deep feedforward neural networks by Glorot and Bengio, 2010
Exact solutions to the nonlinear dynamics of learning in deep linear neural networks by Saxe et al, 2013
Random walk initialization for training very deep feedforward networks by Sussillo and Abbott, 2014
Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification by He et al., 2015
Data-dependent Initializations of Convolutional Neural Networks by Krähenbühl et al., 2015
All you need is a good init, Mishkin and Matas, 2015
……

2.4 Sparse initialization. 系数初始化

其思想是先将权重初始设置为全部都是0，但是为了避免2.1叙述的情况，打破初始对称，每个神经单元只能随机的与固定个数的神经单元连接（比如经典的选取10个的方法）。

2.5 截距的初始化

截距或者biase的初始化可以使用0，因为w的设置已经使对称失效了，在使用ReLU时有人会设置为较小的数例如0.01，但是这样设置会不会有好处还没有确切的定论。

2.6 推荐的方法

推荐使用ReLU单元和w = np.random.randn(n) * sqrt(2.0/n的初始化设置方法。

2.7 Batch Normalization

这是一种近期才出现的技术，提出者是Ioffe 和Szegedy，效果不错，连接在这里arXiv。它强制将激活值在训练前设置为高斯分布，他在全连接层和激活函数层中间插入了一层Batch Normalization层. 现在batch normalization的使用已经比较广泛了，具体设置方法请看前面连接的论文,它具有以下优点：
1. 提高了梯度的传递性
2. 可以允许更高的学习速率
3. 降低了对于初始值的依赖性
4. 以regularization的形式起作用，可能稍微会对dropout的需求
另外，Batch normailization可以被理解为在每层之前做一下预处理, 但是却集成到了神经网络中去了。

3 Regularization 规则化

3.1 L2

L2 regularization可能是最常见的规则化方法了，其手段就是将每个w都加入一项 12λw2 ,这里的1/2是为了在求导的时候能够约去2，其作用相当于W += -lambda * W,让w向0的方向线性降低。它倾向于使各个权重变得分散均匀，也就是倾向于使各个输入值都可以被利用。

3.2 L1

L1是加入了 λ|w| 项，其好处是可以得到稀疏矩阵，留住重要的输入，去除噪音，L1可以和L2 混用这时也称作Elastic net regularization。如果不是想明确特征的选择，一般L2的效果要比L1要好。

3.3 Max norm constraints

最大范数约束主要思路是安照正常进行update，只不过每次更新之后检查其范数是否大约了设定值 ∥w⃗ ∥2<c ,c的经典取值是3或者4.有人说效果还可以。

3.4 Dropout

这是一种简单高效常用的方法，与前面的三种方法互补，由 Srivastava等提出的。文章在这里Dropout: A Simple Way to Prevent Neural Networks from Overfitting(PDF)。
这种方法的思想是在训练时候只是一部分的神经单元工作，如图：

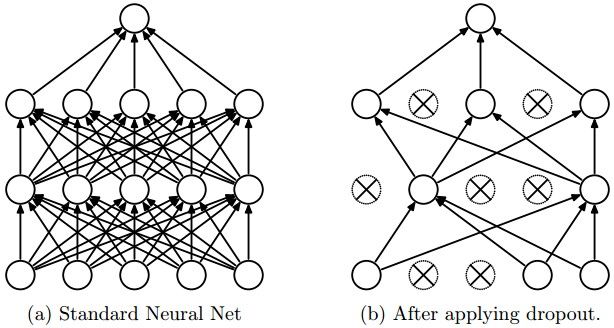
神经单元可以被使用的概率是P（是一个超参数）或者是0，其测试的时候全部的神经元都是可以利用的，这时候相当于ensemble。
下面是一个三层网络的简易过程：

""" Vanilla Dropout: Not recommended implementation (see notes below) """

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  """ X contains the data """

  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)#相当于将矩阵的最小值变为0，where（x>0,0）
  U1 = np.random.rand(*H1.shape) < p # first dropout mask注意星号哦
  H1 *= U1 # drop!注意*=
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = np.random.rand(*H2.shape) < p # second dropout mask
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3

  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)

def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations注意生成了一个p
  H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activations
  out = np.dot(W3, H2) + b3

上面我们没有对输入层进行dropout（也可以做），输出层加入了p这一乘积项，这是因为训练的时候某个神经单元被使用的概率是p，如果他的输出是x那么他训练时输出值的期望只是px，所以在预测阶段要乘以p，但是并不推荐这样做。因为在预测阶段进行操作无异于增加了预测响应时间。我问使用 inverted dropout来解决这个问题。
其方法是在预测时不再乘以p，而是在预测时除以p。

""" Inverted Dropout: Recommended implementation example. We drop and scale at train time and don't do anything at test time. """

p = 0.5 # probability of keeping a unit active. higher = less dropout

def train_step(X):
  # forward pass for example 3-layer neural network
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!这是重点，重点，点，点，点
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3

  # backward pass: compute gradients... (not shown)
  # perform parameter update... (not shown)

def predict(X):
  # ensembled forward pass
  H1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessary
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  out = np.dot(W3, H2) + b3

相关书籍：
1. Dropout paper by Srivastava et al. 2014.
2. Dropout Training as Adaptive Regularization: “we show that the dropout regularizer is first-order equivalent to an L2 regularizer applied after scaling the features by an estimate of the inverse diagonal Fisher information matrix”.

3.5 Theme of noise in forward pass

类似于dropout还有很多类似的方法，比如dropconnect.

3.6 bias regularization

bias不与输入变量直接相乘，不能控制数据对最终目标的影响，所以表示一般不用regularization，但是它的数量相对于w很少，约束下也不会有太大的影响。

3.7 Per-layer regularization.

很少有这样对每层加不同约束的。

3.8 应用

1. 最常见的是使用一个使用cv优化之后的单独的L2约束
2. 可以使用dropout之后用L2，p可以选用0.5也可以选别的值，但是需要在验证集上检验下。

4 损失函数 loss functions

我们已经考虑loss function里的regularization loss 还有一部分 data loss还没有考虑.损失函数是考虑每个案例的损失的平均值 L=1N∑iLi ,这里设神经网络的激活函数为 f=f(xi;W) ,下面按照分类和回归问题分析损失函数。

4.1 分类问题

我们目前讨论的分类问题一般只有一个正确答案，常用的有svm和softmax的损失函数。svm的分类损失函数是：

Li=∑j≠yimax(0,fj−fyi+1)

或者

Li=∑j≠yimax(0,fj−fyi+1)2

softmax的损失函数是：

Li=−log⎛⎝efyi∑jefj⎞⎠

4.1.2大量类别问题

在进行文字分类等有很多类别的时候可以用Hierarchical Softmax的方法，其栗子在这里，他先创建一棵类别树，每一个节点用于softmax，树的结构对分类效果影响很大，需要具体问题具体分析。

4.1.3多属性类别

同一个物体可能有多重属性，其类别也就可能有多个，解决方法有：
1. 多个二分类器，其损失函数为

Li=∑jmax(0,1−yijfj)

j代表类别，yij代表第i个example是否属于j类（取1或者-1），fj是预测的score function。
2. 建立多个logistic regression。

Li=∑jyijlog(σ(fj))+(1−yij)log(1−σ(fj))

其中 σ 是sigmoid函数，对f求导得到： ∂Li/∂fj=yij−σ(fj)

4.2 regression回归

L2形式：

Li=∥f−yi∥22

l2求导方便
L1形式：

Li=∥f−yi∥1=∑j∣fj−(yi)j∣

设 δi,j 是i-th样本的第j个特征相对于真实值的差距，这时 ∂Li/∂fj 要么等于 δi,j 的L2范数，要么等于 sign（δi,j） ，所以对得分函数的梯度一般要么直接使用delta的比例，要么修正之后只集成sign的部分。

4.3 注意

1. L2 loss的求解比稳定的损失如softmax的损失要更难优化；
2. softmax的得分多少并不重要，只有在量级合适的时候才有意义；
3. L2 loss 因为outliers可能会引入巨大的梯度所以可能不稳定
4. 面对regression先看能不能化为classification
5. 对regression的L2 loss不宜使用dropout。

4.4 Structured prediction.

结构化预测(structured prediction)是由SVM发展而来的。，结构化问题的例子有很多：给定一个句子，找出它对应的依存树(dependency tree)；对一个图进行分割(image segmentation)等。结构化预测通过修改SVM的约束条件以及目标函数，将SVM从二分类问题扩展到可以预测结构化问题。这类问题一般很难用纯数学去计算，具体内容不再本课程范围内，这里有一篇相关的文章，及维基百科。

总结