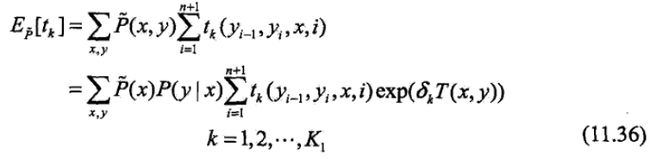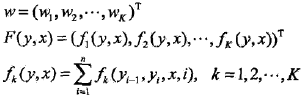条件随机场(CRF) - 4 - 学习方法和预测算法(维特比算法)
声明:
1,本篇为个人对《2012.李航.统计学习方法.pdf》的学习总结,不得用作商用,欢迎转载,但请注明出处(即:本帖地址)。
2,由于本人在学习初始时有很多数学知识都已忘记,所以为了弄懂其中的内容查阅了很多资料,所以里面应该会有引用其他帖子的小部分内容,如果原作者看到可以私信我,我会将您的帖子的地址付到下面。
3,如果有内容错误或不准确欢迎大家指正。
4,如果能帮到你,那真是太好了。
学习方法
条件随机场模型实际上是定义在时序数据上的对数线性模型,其学习方法包括极大似然估计和正则化的极大似然估计。
具体的优化实现算法有改进的迭代尺度法IIS、梯度下降法以及拟牛顿法。
改进的迭代尺度法(IIS)
已知训练数据集,由此可知经验概率分布
可以通过极大化训练数据的对数似然函数来求模型参数。
训练数据的对数似然函数为
当Pw是一个由
给出的条件随机场模型时,对数似然函数为
IIS通过迭代的方法不断优化对数似然函数改变量的下界,达到极大化对数似然函数的目的。
假设模型的当前参数向量为w=(w1,w2, ..., wK)T,向量的增量为δ=(δ1,δ2, ..., δK)T,更新参数向量为w +δ=(w1+δ1, w2 +δ2, ..., wk +δk)T。在每步迭代过程中,IIS通过一次求解下面的11.36和11.37,得到δ=(δ1,δ2, ..., δK)T。
关于转移特征tk的更新方程为:
关于状态特征sl的更新方程为:
这里T(x, y)是在数据(x, y)中出现所有特征数的综合:
于是算法整理如下。
算法:条件随机场模型学习的改进的迭代尺度法
输入:特征函数t1,t2, ..., tK1,s1, s2, ..., sK2;经验分布![]()
输出:参数估计值 ![]() ;模型。
;模型。
过程:
拟牛顿法
对于条件随机场模型
学习的优化目标函数是
其梯度函数是
拟牛顿法的BFGS算法如下:
算法:条件随机场模型学习的BFGS算法
预测算法
条件随机场的预测问题是给定义条件随机场P(Y|X)和输入序列(观测序列)x,求条件概率最大的输出序列(标记序列)y*,即对观测序列进行标注。
条件随机场的预测算法是著名的维特比算法。
在介绍维特比算法之前,我先用通俗的语言描述下它。
假设我们遇到了这么个问题:
大学时你让室友帮你带饭(如果你上过大学,别告诉我你别干过这事....),然后你室友问你想吃啥?你回答:“你吃啥我吃啥,不过回来时帮忙带瓶雪碧,谢啦”。于是有趣的事就发生了:你室友给你带回了饭和雪碧并兴高采烈的说:“我去,食堂换大厨了,那个小卖部的收银员换成了个漂亮妹子!!”然后你问他:“你去的哪个食堂和小卖部?”,他想了想回答:“你猜。”
好了,你猜吧~
我猜你妹啊(╯‵□′)╯︵┻━┻
嘛,先别慌掀桌,不管如何你室友帮你带了饭,所以咱们就满足下他那小小的恶作剧,就当做是给他跑腿的辛苦费好了。
PS:假设你学校有2个小卖部和2个食堂。
于是,mission start!
首先,问他:你先去得小卖部?他回答:是的。
OK,买东西的先后顺序搞定了。
那就开始想:
第一步:从宿舍到小卖部A和B的距离都差不多,不好判断;
第二步:从小卖部A、B到食堂1、2有四种路线(A1, A2,B1, B2),然后这四种路线中到食堂1最短的是B1,到食堂2最短的是A2;
第三步:看看他给带来的饭,嗯....这个饭我记得食堂1有卖,食堂2不知道,就当没有吧,那就假设他去的是食堂1;
第四步:既然他去的是食堂1,按照这货的习惯,绝壁选个最近的小卖部,所以他会选择距离食堂1最近的小卖部B;
第五步:对他说:“你先去小卖部B然后去食堂1对吧”,他说:“我次奥,你咋知道的”。
好了,例子举完了,我们来看看维特比算法,其实维特比算法就是上面的过程:先从前向后推出一步步路径的最大可能(从出发点到第一个目的地集合的每个可能性,从第一个目的地集合到第二个目的地集合的每个可能性,以此类推),然后在确定终点之后在反过来选择前面的路径(确定终点是食堂1了,那因为室友选择到食堂1的路线B1的可能性大于路线A1,所以按照路线,终点的上一个目的地集合里,室友就选择的小卖部B,以此类推),最终确定最优路径。
现在,你对维特比算法是什么就有概念了吧,下面来看看其数学描述。
在上面的例子中你会发现:“每个路径可能性”的确定是十分重要的。既然如此,我们就得看看条件随机场的“每个路径可能性”,即:条件随机场的局部特征向量。
由
可得:
于是,条件随机场的预测问题成为求非规范化概率最大的最优路径问题
![]()
这里,路径表示标记序列,其中
注意,这时只需计算非规范化概率,而不必计算概论,可以大大提高效率。
为了求解最优路径,将11.52式写成如下形式:
其中
就是局部特征向量。
下面叙述维特比算法。
首先求出位置1的各个标记j=1,2,...,m的非规范化概率:
PS:m指的位置1的数量,比如上面的例子中位置1只有2个(小卖部1和小卖部2),那m就为2。下面同理。
一般的,有递推公式,求出到位置i的各个标记l=1,2,...,m的非规范化概率的最大值,同时记录非规范化概率最大值的路径:
直到i=n时终止。这时求得非规范化概率的最大值为:
最优路径的终点
由此最优路径终点返回
求得最优路径
y*= (y1*, y2*, ..., yn*)T。
综上所述,得到条件随机场预测的维特比算法。
算法:条件随机场预测的维特比算法
下面通过一个例子来说明维特比算法。
例子
对于之前用过的例11.1(如下图),用维特比算法求给定的输入序列(观测序列)x对应的输出序列(标记序列)y* = (y1*, y2*, y3*);
解:
下面是步骤截图,在后面我会有讲解
解释:
首先,例11.1实际上就是在叙述下图:
第一步初始化:
因为y1=1和y1=2是最初,所以就不用考虑转移的情况了(实际上也没有“表达从y0转移到y1的情况”的t函数(转移函数)),直接从状态函数(s函数中找),发现,s1和s2分别对应y1=1和y1=2,说明y1=1和y1=2这个状态都是存在的,而s1和s2的权值分别是1和0.5,且上面列出的s函数们和t函数们值都为1,所以y1=1和y2=1的可能性分别是1和0.5。
所以,到达y1的非规范化概率最大值为:δ1(1) = 1,δ1(2) = 0.5。
第二步递推:
i=2(达第二处目的地集合{y2=1, y2=2}):
首先是路线(仅说明到达y2=1的情况):
上图可知,到达y2=1的路线有如下几条:
路线1:从y1=1出发 ----(经过t2)---->到达y2=1;
路线2:从y1=2出发 ----(经过t4)---->到达y2=1;
接着是状态(仅说明到达y2=1的情况):
根据题目可知:i=2时的状态函数只有s2和s3,而y2=1对应的函数是s3
所以到达y2=1的非规范化概率最大值为:
δ2(1) = max{1+λ2t2 + u3s3,0.5 + λ4t4 + u3s3}= 2.4
PS:这里相对于原题我多加了个u3s3,因为用上面这种思路可以解释通其他所有的δi,如果这种想法有问题,还请告知,不胜感激。
非规范化概率最大值的路径为:
ψ2(1) = 1
δ2(2)同理。
i=3也一样(只不过对于δ3(1)中的u5s5,我认为应该是u3s3,先不说s3对应的是y3=1的情况,而且原题中根本没有s5函数)。
第三部终止:
这步就简单了,在δ3(l)中δ3(1) = 4.3最大,所以y3中取1的可能性最大,即y3*=1。
第四步返回:
然后反着推:
从y2的哪个值到y3可能性最大呢?在第二部已经解出:ψ3(1) = 2,即y2到达y3=1的路线中权值最大的是y2=2,即y2*=2。
同理,从y1=1到y2=2的可能性最大,即y1*=1。
最后就得到标记序列
y*= (y1*, y2*, y3*)= (1, 2, 1)