STL源码笔记(17)—二叉排序树BST(C++封装)
二叉排序树BST
STL中还有一类非常重要的容器,就是关联容器,比如map啊set啊等等,这些容器说实话,在应用层上还不能完全得心应手(比如几种容器效率的考虑等等),更别说源码了,因此这一部分打算稳扎稳打,好好做做笔记研究一番。
说到关联容器,我们想到了什么AVL树,红黑树等等,但大多时候我们仅仅局限于知道其名字,或者知道其概念,俗话说“talk is cheap,show me the code”,因此,我打算从他们的祖爷爷二叉排序树开始下手。(其实,侯老师的书上也是这么安排的哈)
1.概念
1.任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
2.任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
3.任意节点的左、右子树也分别为二叉查找树;
4.没有键值相等的节点。
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为 O(logn) 。二叉查找树是基础性数据结构,用于构建更为抽象的数据结构,如集合、multiset、关联数组等。
2.性质
1.中序遍历是一个升序的有序序列。
2.搜索、插入、删除的复杂度等于树高,期望 O(logn) ,最坏O(n)(数列有序,树退化成线性表)。
3.二叉排序树的实现
既然看到此,不如试着实现一下二叉排序树,主要需要包含这些操作:构建二叉排序树输入一个序列输出一个二叉排序树,插入、删除节点。
写代码之前考虑的问题:
1.二叉排序树的插入一定是在叶子节点处。
2.二叉排序树的删除需要考虑三种情况:
a)待删除节点在叶子节点处
直接另其父节点相应指针制空,并删除该节点即可。
b)待删除节点只含有一个孩子(左子树为空或者右子树为空)
将待删除节点父节点对应指针指向待删除节点的孩子节点。
c)待删除节点即包含左右孩子都不为空
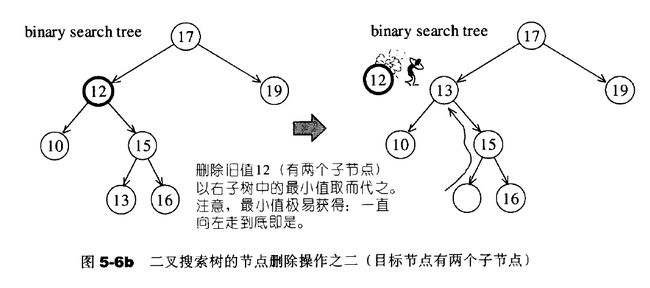
找到待删除节点的右子树的最小值(右子树一路向左),并将该值替换待删除节点的值,最后删除最小值原本所在位置的节点(叶子节点)。3.二叉排序树的中序遍历是升序。
4.摈弃以前的C语言写法,我这次想把BST封装成一个C++类,虽然困难重重,勉强实现了吧。
5.既然是C++类,在析构函数中做所有节点内存释放处理(最后一个根节点需要特殊处理)。
上述5个问题中除了对C++的熟悉程度外,涉及BST算法部分最麻烦的就是删除操作了,因为它考虑的情况比较多,这里贴出侯老师书中的示意图方便理解:
目标节点只有一个孩子节点
目标节点有两个子节点
代码
编译运行环境:Visual Studio 2013,Windows 7 32 bits
(1)二叉排序树的节点数据结构
//BSTNode.h
#ifndef __BSTNODE_H__
#define __BSTNODE_H__
#include<iostream>
class BSTNode{
public:
BSTNode();
BSTNode(int val);
int value;
BSTNode *lchild;
BSTNode *rchild;
};
#endif
//--------------------------------------------
//--------------------------------------------
//--------------------------------------------
//BSTNode.cpp
#include "BSTNode.h"
BSTNode::BSTNode()
{
value = 0;
lchild = NULL;
rchild = NULL;
}
BSTNode::BSTNode(int val)
{
value = val;
lchild = NULL;
rchild = NULL;
}(2)二叉排序树的C++类封装
//BST.h
#ifndef __BST_H__
#define __BST_H__
#include "BSTNode.h"
#include <vector>
#include <iostream>
class BSTNode;
class BST
{
//说明:
//为了数据结构私有化,不为外部访问,这里提供一些私有内部函数实现真正的操作以"__"开头。
//对于public的接口来说,只需要直接调用内部函数即可
private:
BSTNode * bstroot;//二叉排序树数据结构
BSTNode * __search(BSTNode* root,const int& key);//查找关键字
BSTNode * __treeMin(BSTNode*const root,BSTNode *&parent);//返回当前节点的最小孩子(一路向左)
BSTNode * __treeMax(BSTNode*const root);//查找最大值(未实现)
bool __Insert( const int &key);//插入节点
bool __Delete(const int &key);//删除删除
bool __isLeaf(BSTNode* const &);//判断是否是叶子节点
bool __isNodeWithTwoChild(BSTNode * const &);//判断是否有两个孩子
void __InorderTraversal(BSTNode *root,std::vector<int>&result);//中序遍历
void __DeleteAllNodes(BSTNode *root);//删除所有节点
public:
//构造函数
BST();//默认构造函数
BST(std::vector<int>arr);
BST(int *arr, int len);
//析构函数
~BST();
bool isEmpty() const;//判断树空
bool search(const int &key);//查找关键字是否存在的对外接口
bool Insert(const int &key);//插入节点的外部接口
bool Delete(const int &key);//删除节点的外部接口
void InorderTraversal(std::vector<int>&);//中序遍历的外部接口
};
#endif(3)二叉排序树C++类实现部分
//BST.cpp
#include "BST.h"
//判断树空
bool BST::isEmpty() const
{
return bstroot == NULL;
}
//判断是否是叶子节点(删除部分用到)
bool BST::__isLeaf(BSTNode*const & root)
{
if ((root->lchild == NULL) && (root->rchild == NULL))
return true;
else
return false;
}
//判断节点是否有两个孩子(删除部分用到)
bool BST::__isNodeWithTwoChild(BSTNode * const & root)
{
if (root->lchild != NULL &&root->rchild != NULL)
return true;
else
return false;
}
//找到当前节点为根的子树中的最小值(删除部分用到,因此返回其父节点和当前节点)
BSTNode * BST::__treeMin(BSTNode*const root,BSTNode *&parent)
{
BSTNode * curr = root;
while (curr->lchild != NULL)
{
parent = curr;
curr = curr->lchild;
}
return curr;
}
//删除节点内部实现
bool BST::__Delete(const int &key)
{
bool found = false;//找到待删除的元素
if (isEmpty())
{
std::cerr << "Binary Search Tree Is Empty" << std::endl;//BST为空
return false;
}
BSTNode * curr = bstroot;
BSTNode *parent = NULL;
while (curr != NULL)//查找待删除节点
{
if (key == curr->value)
{
found = true;
break;
}
else
{
parent = curr;
if (key < curr->value)
curr = curr->lchild;
else
curr = curr->rchild;
}
}
if (!found)
{
std::cerr << "KeyValue Not Found" << std::endl;
return false;
}
if (NULL == parent)//删除最后一个节点(根节点需要特殊处理)
{
bstroot = NULL;
delete curr;
return true;
}
//对于待删除的节点有三种可能:
//1.叶子节点
//2.只包含左子树或者右子树(单个孩子)
//3.既包含左子树又包含右子树
//删除节点的时候需要分3种情况进行考虑
if (__isLeaf(curr))//叶子节点
{
if (parent->lchild == curr)
parent->lchild = NULL;
else
parent->rchild = NULL;
delete curr;
return true;
}//end if
else if (__isNodeWithTwoChild(curr))//有两个孩子的节点
{
//以当前节点的右子树中的最小值取代它
BSTNode*parent=curr;
BSTNode *tmp = __treeMin(curr->rchild,parent);
curr->value = tmp->value;
if (parent->rchild == tmp)
parent->rchild = NULL;
else
parent->lchild = NULL;
delete tmp;
return true;
}//end else-if
else//只有一个孩子的节点
{
if (curr->lchild != NULL)//只有左孩子
{
if (parent->lchild == curr)
{
parent->lchild = curr->lchild;
delete curr;
return true;
}
else
{
parent->rchild = curr->lchild;
delete curr;
return true;
}
}
if (curr->rchild != NULL)//只有右孩子
{
if (parent->lchild == curr)
{
parent->lchild = curr->rchild;
delete curr;
return true;
}
else
{
parent->rchild = curr->rchild;
delete curr;
return true;
}
}
}//end else
return false;
}
//删除操作的外部接口
bool BST::Delete(const int &key)
{
return __Delete(key);
}
//插入节点的内部实现,插入操作一定都在叶子节点处。
bool BST::__Insert(const int & key)
{
BSTNode* t = new BSTNode(key);//临时节点
BSTNode*parent = NULL;
if (isEmpty())//新树
{
bstroot = t;
return true;
}
else
{
BSTNode* curr;
curr = bstroot;
while (curr)
{
//插入位置都位于叶子节点处
parent = curr;
if (t->value > curr->value)
curr = curr->rchild;
else
curr = curr->lchild;
}
if (t->value < parent->value)
{
parent->lchild = t;
return true;
}
else
{
parent->rchild = t;
return true;
}
}
return false;
}
//插入节点的外部接口
bool BST::Insert(const int &key)
{
return __Insert(key);
}
//构造函数
BST::BST()//默认构造函数
{
bstroot = NULL;
}
BST::BST(int*arr, int len)//数组构造
{
bstroot = NULL;
for (int i = 0; i < len; i++)
{
__Insert(*(arr + i));
}
}
BST::BST(std::vector<int>arr)//容器构造
{
bstroot = NULL;
for (int i = 0; i < (int)arr.size(); i++)
{
__Insert(arr[i]);
}
}
//内部查找函数
//递归调用
BSTNode* BST::__search(BSTNode*root,const int& key)
{
if (NULL == root)
return NULL;
if (key == root->value)
return root;
else if (key < root->value)
return __search(root->lchild, key);
else
return __search(root->rchild, key);
}
//查找函数接口
bool BST::search(const int& key)
{
BSTNode*t = __search(bstroot, key);
return t == NULL ? false : true;
}
//中序遍历内部实现
void BST::__InorderTraversal(BSTNode *root,std::vector<int>&result)
{
if (NULL == root)
return;
__InorderTraversal(root->lchild, result);
std::cout << root->value << " ";
result.push_back(root->value);
__InorderTraversal(root->rchild, result);
}
//中序遍历接口,vector保存遍历结果
void BST::InorderTraversal(std::vector<int>&result)
{
__InorderTraversal(bstroot, result);
}
//删除所有节点(析构用)
void BST::__DeleteAllNodes(BSTNode *root)
{
if (root == NULL)
{
return;
}
__DeleteAllNodes(root->lchild);
__DeleteAllNodes(root->rchild);
__Delete(root->value);
}
//析构函数
BST::~BST()
{
BSTNode*curr = bstroot;
__DeleteAllNodes(curr);
}(4)二叉排序树的测试代码
//main.cpp
#include "BST.h"
int main()
{
std::vector<int>vec = { 8,6,2,5,1,3,7 };
BST bst(vec);
bst.Delete(9);//Not found
bst.Insert(4);
bool found=bst.search(4);
if (!found)
std::cout << "not found" << std::endl;
else
std::cout << "found!" << std::endl;
std::vector<int>result;
bst.InorderTraversal(result);
std::cout << std::endl;
for (int i = 0; i < result.size(); i++)
{
std::cout << result[i] << " ";
}
std::cout << std::endl;
system("pause");
return 0;
}4.参考
http://www.cplusplus.com/forum/general/1551/