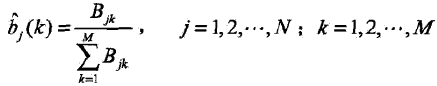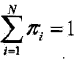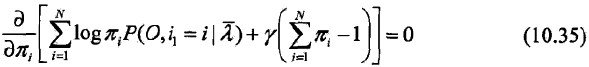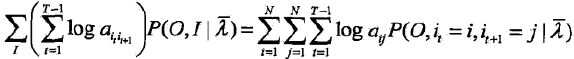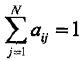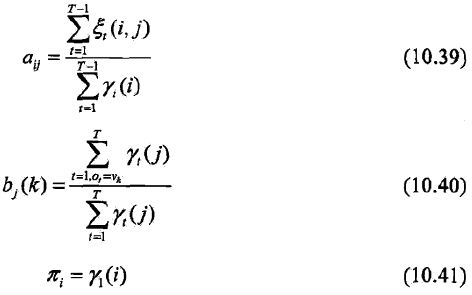隐马尔可夫模型(HMM) - 3 - 学习方法

声明：

         1，本篇为个人对《2012.李航.统计学习方法.pdf》的学习总结，不得用作商用，欢迎转载，但请注明出处（即：本帖地址）。

         2，由于本人在学习初始时有很多数学知识都已忘记，所以为了弄懂其中的内容查阅了很多资料，所以里面应该会有引用其他帖子的小部分内容，如果原作者看到可以私信我，我会将您的帖子的地址付到下面。

         3，如果有内容错误或不准确欢迎大家指正。

         4，如果能帮到你，那真是太好了。

 

         隐马尔可夫模型的学习根据训练数据的不同分为监督学习和非监督学习。

                   若训练数据包括观测序列和对应的状态序列，则可进行监督学习；

                   若训练数据仅有观测序列，那就要用非监督学习了。

监督学习方法

         假设已给训练数据包含S个长度相同的观测序列和对应的状态序列{(O₁, I₁), (O₂, I₂),..., (O_s, I_s)}，那么可以利用极大似然估计法来估计隐马尔可夫模型的参数。

         1，转移概率aij的估计

                   设样本中时刻t处于状态i，时刻t+1处于状态j的频数为A_ij，那么状态转移概率a_ij的估计是

                           

         2，观测概率b_j(k)的估计

                   设样本中状态为j且观测为k的频数是B_jk，那么状态为j且观测为k的概率b_j(k)的估计是

                           

         3，初始状态概率πi的估计为S个样本中初始状态为qi的频率。

         由于监督学习需要使用训练数据，而人工标注训练数据往往代价很高，所以有时会利用非监督学习的方法。

Baum-welch算法

         Baum-welch算法就是一个非监督学习算法，话说这个就是EM算法....

         不过因为EM算法在教材中已经被单独列出一章，所以这里就是对EM算法的应用。而因为我也单独对EM算法进行了总结，所以这里不会再对下面列出的EM算法中的步骤做过多讲解，如果你还不知道EM算法的话，请去看看我总结的“机器学习 -- EM算法 - 1 - 介绍”。

         好了，开始。

         现在假设给定的训练数据只包含S个长度为T的观测序列{o₁, o₂, ..., o_s}而没有对应的状态序列，然后目标是学习隐马尔可夫模型λ= (A, B,π)的参数。

         我们将观测序列数据看做观测数据O，状态序列数据看做不可观测的隐数据I，那么隐马尔可夫模型事实上是一个含有隐变量的概率模型

                  

         它的参数学习可以由EM算法实现。

 推导：

         1，确定完全数据的对数似然函数

         把所有观测数据写成O ={o₁, o₂, ..., o_T}，所有隐数据写成I ={i₁, i₂, ..., i_T}，完全数据是(O, I)= (o₁, o₂, ..., o_T, i₁, i₂,..., i_T)。完全数据的对数似然函数是logP(O, I |λ)。

         2，EM算法的E步，求Q函数

                 

PS:上式的推导过程是这样(为了少截几张图，我就用Z代替上式中的“λ杠”，且求和符号用“[和]”代替)                    Q(λ,Z)  = [和]logP(O, I|λ)P(I|O,Z)                                 = [和]logP(O,I|λ)[P(O,I|Z)/P(O|Z)]                   因为1/P(O|Z)即不含隐参数，而且Z在Q函数的定义中是已求出的，所以这一项对λ而言是常数因子，因此可以略去。                   最后，在略去了常熟因子1/P(O|Z)之后就有了上面的Q函数。

         其中Q(λ,λ杠)中的“λ杠”是隐马尔可夫模型参数的当前估计值，λ是要极大化的隐马尔可夫模型参数。

                 

                           PS：P(O,I|λ)的得出见“隐马尔可夫模型(HMM)- 2 - 概率计算方法”中的“直接计算法”

         于是Q(λ,λ杠)可以写成：

                    

         上式中的求和都是对所有训练数据的序列总长度T进行的。

         3，EM算法的M步：极大化Q(λ,λ杠)求模型参数A, B,π

         由于要极大化的参数在10.34式中单独地出现在3个项里，所以只需对各项分别极大化。

                   a，10.34式的第一项可以写成：

                           

                   注意πi满足约束条件

                           

                   利用拉格朗日乘子法，写出拉格朗日函数：

                           

                   对其求偏导并令结果为0

                           

                   得

                           

                   上式的两项均对i求和，可以得到γ

                           

                   于是

                           

                   b，10.34式的第二项可以写成

                           

                   类似第一项，应用具有约束条件

                           

                   的拉格朗日乘子发可以求出

                           

                   c，10.34式的第三项为

                           

                   同样用拉格朗日乘子法，约束条件时

                           

                   注意，只有在o_t= v_k时b_j(o_t)对b_j(k)的偏导数才不为0，以O(o_t= v_k)表示，求得：

                           

                   d，Baum-welch模型参数的估计公式

                   将10.36 ~10.38中的各概率分别用γ(i)，ξ(i, j)表示，则可将相应的公式写成

                           

                   其中γ(i)，ξ(i, j)分别由“隐马尔可夫模型(HMM)- 2 - 概率计算方法”中的“一些概率与期望值的计算”部分给出。

         最终，10.39 ~10.41式就是Baum-welch算法，它是EM算法在隐马尔可夫模型学习中的具体实现，由Baum和Welch提出。

         于是将上面的内容整理后，Baum-welch算法如下

 Baum-welch算法

         输入：观测数据O = {o₁,o₂, ..., o_T}；

         输出：隐马尔可夫模型参数。

         过程：