POJ1003 Hangover
题目:
Description
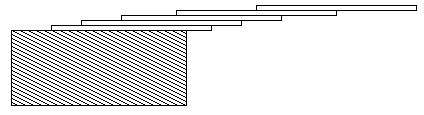
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.
Input
Output
Sample Input
1.00 3.71 0.04 5.19 0.00
Sample Output
3 card(s) 61 card(s) 1 card(s) 273 card(s)
思路:
题目很简单,大意为:
输入一个浮点数,记为c,找出累加式1/2 + 1/3 + 1/4 + ... + 1/(n + 1)大于等于c的最小的n,0.01<=c<=5.20,输入0.00代表输入结束。
也就是求1/2+1/3+1/4+...+1/(n+1),当n大于等于多少时,该式子的值大于等于input的值。
代码:
#include<iostream>
using namespace std;
int main(){
//考察s=1/2+1/3+1/4+...1/(n+1),当n>=某正整数时,s能达到input的值,此时output该正整数
/* 首先看看要到达5.20,需要多少张卡片,答案:i输出为278,也就是需要277张卡片
int i=2;
double result=0;
while(result<5.2){
result+=1/(double)i;
i++;
}
cout<<i<<endl;
*/
double s;
while(cin>>s){
if(s==0.0)
break;
int i=1;
double result=0;
while(result<s){
i++;
result+=1/(double)i;
}
//为什么是i-1呢,因为最后一项是1/i的话,也就是1/(n+1),这样的话n就是i-1
cout<<(i-1)<<" card(s)"<<endl;
}
return 0;
}
这种暴力破的方式,最后时间居然为0ms,大概是因为input<=5.20,所以循环次数最多也为277吧。。。
后来看别人的代码,大家好像都是暴力破的,唯一一个有点不太一样的,是先算出1/2加到1/300的所有的和存入数组,(因为最多是277,所以大概那人就直接取整用300做了),然后将input的值在数组里一个个比较。
#include <stdio.h>
int main()
{
float res[300] = {0,0.5},c;
int i,num = 0;
for (i = 2;i< 300;i++)
res[i] = res[i-1] + 1.0/(i+1);
while(scanf("%f",&c) && c)
{
for(i = 1;i < 300;i++)
{
if(res[i] >= c)
{
printf("%d card(s)\n",i);
break;
}
}
}
return 0;
}
试了去POJ上跑了一下他的代码,时间也为0ms。所以差不多
看了下他的说明,他认为因为数组长度很短,只有300,所以直接在数组中查的话,与二分查找的时间不会有太大差别。而当数组长度大的时候,就应该用二分查找,这样更快。