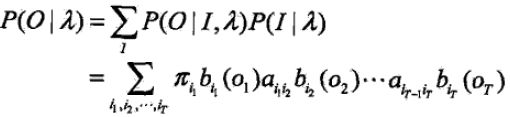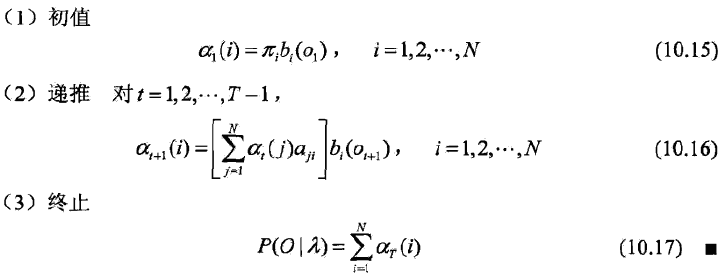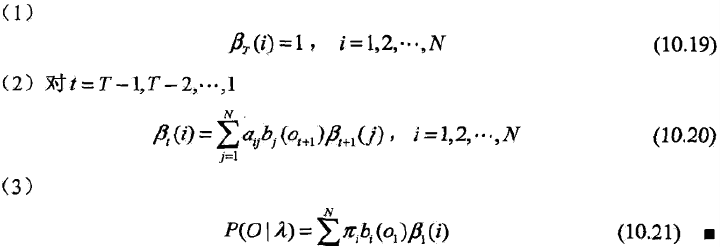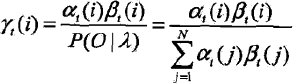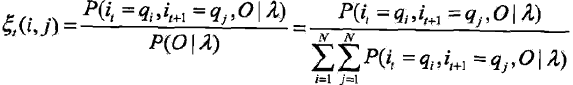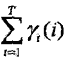隐马尔可夫模型(HMM) - 2 - 概率计算方法
声明:
1,本篇为个人对《2012.李航.统计学习方法.pdf》的学习总结,不得用作商用,欢迎转载,但请注明出处(即:本帖地址)。
2,由于本人在学习初始时有很多数学知识都已忘记,所以为了弄懂其中的内容查阅了很多资料,所以里面应该会有引用其他帖子的小部分内容,如果原作者看到可以私信我,我会将您的帖子的地址付到下面。
3,如果有内容错误或不准确欢迎大家指正。
4,如果能帮到你,那真是太好了。
本章介绍隐马尔可夫模型中概率计算问题的算符。
计算观测序列概率P(O|λ)的算法包括前向算符和后向算法,不过在此之前先介绍下概念上可行但计算上不可行的直接计算法。
直接计算法
给定模型λ= (A, B,π)和观测序列O = (o1,o2, ..., oT),计算测序列O出现的概率P(O|λ)。最直接的方法是按概率功率直接计算。
思想:
通过列举所有可能的长度为T的状态序列I = (i1,i2, ..., iT),求各个状态序列I与观测序列O = (o1, o2, ..., oT)的联合概率P(O,I|λ),然后对所有可能的状态序列求和,得到P(O|λ)。
过程:
1,状态序列I = (i1,i2, ..., iT)的概率是
即:状态1的概率*状态1转到状态2的概率*...*状态T-1转到状态T的概率
PS:上式中的π对应初始概率分布,aij对应状态转移概率分布的矩阵,若看不懂上面的内容,则请对照着“隐马尔可夫模型(HMM) - 1 - 基本概念”中的这两个概念看。
2,对固定的状态序列I =(i1, i2, ..., iT),观测序列O = (o1, o2, ..., oT)的概率是
即:第一个观测的概率*第二个观测的概率*...*第T个观测的概率
3,O和I同时出现的概率为
PS:这个利用了条件概率公式
4,对所有的状态序列I求和,得到观测序列O的概率P(O|λ),即
但是(1式)的计算量很大,是O(TNT)阶,这种算法不可行。
下面介绍计算观测序列概率P(O|λ)的有效方法:前向-后向算法。
前向算法
首先定义前向概率
定义(前向概率)
给定隐马尔可夫模型λ,定义到时刻t部分观测序列为o1, o2, ..., ot,且状态为qi的概率为前向概率,记做
at(i)= P(o1, o2, ..., ot, it = qi |λ)
举个例子:
从A、B这两个硬币中随机拿一个投掷看正反面,A、B硬币抓取的概率一样,即都是0.5,但因为A、B的材质原因导致这两个硬币正面向上的概率是0.6,反面向上的概率是0.4。
因此前向概率
a4(2)= P(正, 正, 反, 正, i4 = q2|λ)
就表示“到时刻4时的观测序列为 o1=正,o2=正,o3=反,o4=正,且第四次投掷的硬币为硬币B(假设q1=硬币A,q2=硬币B)的概率”
在知道了前向概率的定义后就可以递推的求前向概率at(i)及观测序列概率P(O|λ)。
算法(观测序列概率的前向算法)
输入:隐马尔科夫模型λ,观测序列O;
输出:观测序列概率P(O|λ)
过程:
解释:
步骤1初始化前向概率,即获得第一个状态和第一个观测的概率,即是初始时刻的状态qi和观测o1的联合概率。又因为达到初始时刻状态qi的概率是πi,根据初始状态qi而产生的观测o1的概率是bi(o1),于是有了10.15式。
步骤2是前向概率的递推公式,计算到时刻t+1部分观测序列为o1, o2, ..., ot, ot+1且在t+1时刻处于状态qi的前向概率。
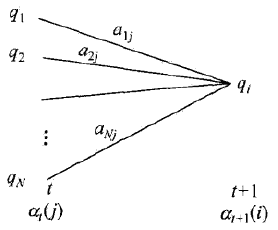
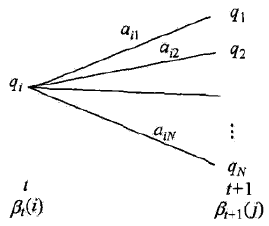
如下图所示:
在10.16式的方括弧里,at(j)表示到时刻t观测到o1,o2, ..., ot并在时刻t处于状态qj的前向概率,那么乘积at(j)aji就是到时刻t观测到o1, o2,..., ot并在时刻t处于状态qj而时刻t+1到达状态qi的联合概率。对这个乘积在时刻t的所有可能的N的状态qj求和,其结果就是到时刻t观测为o1, o2, ..., ot并在时刻t+1处于状态qi的联合概率。
有点绕?
其实是这样,“at(j)aji是到时刻t观测到o1, o2,..., ot并在时刻t处于状态qj而时刻t+1到达状态qi的联合概率”这个没问题吧(有问题我就没办法了..你在多读几遍这句话好好想想),但在时刻t+1之前到底是哪个状态谁也不知道,可能是状态q1,可能是状态q2,可能是状态qj,也可能是状态qN,那我要把所有的可能性包括在内,于是乎对所有的at(j)aji求和,其中j = 1, 2, ..., N,于是就有了方括弧里的内容。
方括弧里的值也观测概率bi(ot+1)的乘积就是时刻t+1观测到o1,o2, ..., ot, ot+1并在时刻t+1处于状态qi的前向概率at+1(i)。
步骤3给出P(O|λ)的计算公式,因为
aT(i)= P(o1, o2, ..., oT, iT = qi|λ)
表示到达时刻T观测到o1, o2,..., oT并在时刻T处于状态qi的前向概率,于是对所有的状态求和即10.17式,就是观测序列概率P(O|λ)的计算公式了。
前向算法高效的关键
前向算法高效的关键是其局部计算前向概率,然后利用路径结构将前向概率“递推”到全局,得到P(O|λ)。
具体地
在时刻t=1,计算a1(i)的N个值(i = 1, 2,..., N);
在时刻t = 1, 2,..., T-1,计算at+1(i)的N个值(i = 1, 2, ..., N),而且每个at+1(i)的计算利用前一时刻的N个at(j)。
减少计算量的原因在于每一次计算直接饮用前一时刻的计算结果,避免重复计算。这样前向概率计算P(O|λ)的计算量是O(N2T)阶的,而不是直接计算的O(TNT)阶。
例子
考虑盒子和球模型λ=(A, B,π),状态集合Q = {1, 2, 3},观测集合V = {红,白},
设T=3,O=(红,白,红),试用前向算法计算P(O|λ)
解:
后向算法
定义(后向概率)
给定隐马尔可夫模型λ,定义在时刻t状态为qi的条件下,从t+1到T的部分观测序列为ot+1, ot+2, ..., oT的概率为后向概率,记做
βt(i) = P(ot+1, ot+2, ..., oT| it= qi,λ)
可以用递推方法求得后向概率βt(i)及观测序列概率P(O|λ)。
算法(观测序列概率的后向算法)
输入:隐马尔可夫模型λ,观测序列O;
输出:观测序列概率P(O|λ)
过程:
解释:
步骤1初始化后向概率,对最终时刻的所有状态qi规定βt(i) = 1。
步骤2是后向概率的递推公式。
如下图所示
为了计算在时刻t状态为qi条件下时刻t+1之后的观测序列为ot+1,ot+2, ..., oT的后向概率βt(i),只需考虑在时刻t+1所有可能的N个状态qj的转移概率(即aij项),以及在此状态下的观测ot+1的观测概率(即bj(ot+1)项),然后概率状态qj之后的观测序列的后向概率(即βt+1(i)项)。
步骤3求P(O|λ)的思路与步骤2一直,只是用初始概率πi代替转移概率。
P(O|λ)的关于前向-后向算法的统一写法
利用前向概率和后向概率的定义,可以将观测序列概率P(O|λ)统一写成
此式当t=1和t=T-1时,分别为10.17式和10.21式。
一些概率与期望值的计算
利用前向概率和后向概率,可以得到关于每个状态和两个状态概率的计算公式。
1,给定模型λ和观测O,在时刻t处于状态qi的概率,记
![]()
可通过前项后项概率计算。事实上,
由前向概率at(i)和后向概率βt(i)定义可知:
at(i)βt(i) = P(it = qi, O |λ)
于是得到
2,给定模型λ和观测O,在时刻t处于状态qi且在时刻t+1处于状态qj的概率,记
可通过前项后项概率计算:
而
所以
3,将γt(i)和ξt(i, j)对各个时刻t求和,可以得到一些有用的期望值:
a,在观测O下状态i出现的期望值
b,在观测O下由状态i转移的期望值
c,在观测O下由状态i转移到状态j的期望值